about
查找
查找:在一些数据元素中,通过一定的方法找出与给定关键字相同的数据元素的过程。
以Python的列表为例。 列表查找(线性表查找): 从列表中查找指定元素:
- 输入: 列表、带查找元素
- 输出: 元素下标(未找到元素时一般返回None或者-1)
内置的列表查找函数:list.index、list.find
通常查找使用顺序查找和二分查找。
排序
排序就是将一组"无序"的记录调整为"有序"的记录序列。
列表排序,将无序列表调整为有序的序列:
- 输入:列表
- 输出:有序列表
有序通常有升序和降序两种。
Python种,列表的内置排序方法是sort,还有个更为强大的内置函数sorted。
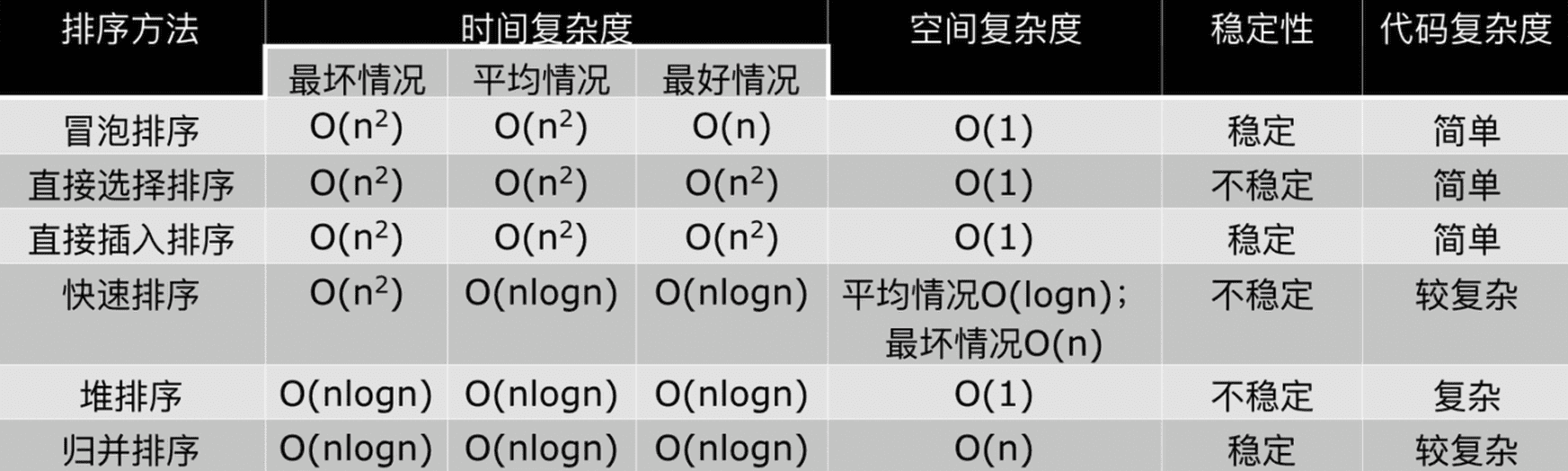
常见的排序算法:
- Low B三人组:冒泡排序、选择排序、插入排序。
- NB三人组:快速排序、堆排序、归并排序。
- 其他排序算法:希尔排序、计数排序、基数排序。
感谢 本篇博客的学习主要参考路飞学城上的算法和数据结构那套视频,感谢路飞学城的精心录制的。 配图有两个摘自知乎,已在相应位置放上链接了,非常感谢,侵删!其他都是我手画的.......
顺序查找
顺序查找(Linear Search): 也叫线性查找,从列表第一个元素开始,顺序的进行搜索,直到找到元素或者搜索到列表最后一个元素为止。
def linear_search(li, value):
for i in li:
if li[i] == value:
return i
else:
return None
linear_search(list(range(100)), 28)顺序查找的时间复杂度是O(n)。
二分查找
二分查找(Binary Search): 又被称为折半查找,从有序列表的初始候选区li[0:n]开始,通过对待查找的值与候选区中间值的比较,可以使候选区每次减少一半。
二分查找的时间复杂度:O(logn)
def binary_search(li, value):
"""
li: 待查找列表
value: 待查找的值
"""
left, right = 0, li.__len__() - 1 # right是列表长度减一
while left <= right: # 表示候选区有值
mid = (left + right) // 2
if li[mid] == value: # 找到了结果,直接返回
return mid
elif li[mid] < value: # value在mid和right之间
left = mid + 1
else:
right = mid - 1
else:
return None
res = binary_search(list(range(100)), 28)
print(res)冒泡
冒泡排序(Bubble Sort)的排序思想:
- 列表每两个相邻的数,如果前面的比后面的大,就交换这两个数。
- 如下面的动图所示,冒泡排序中,可以将列表分为有序区和无序区两部分。
- 一趟排序完成后,则无序区减少一个数,有序区增加一个数。
- 每一趟会选出最大的一个数到有序区,这也意味着无序区减少一个数。
- 那如果有长度为n的列表,采用冒泡排序一共走了多少趟呢?答案是n-1趟,因为最后一趟不用走了,已经都是有序的了。
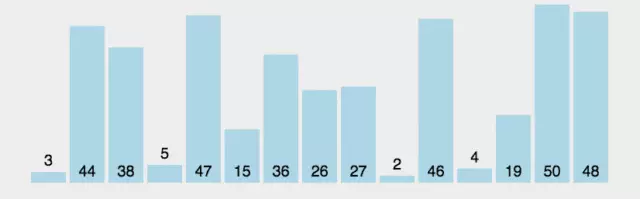
图片摘自:https://zhuanlan.zhihu.com/p/40695917
代码怎么写呢?关键点是趟和无序区的范围。
def bubble_sort(li):
""" 冒泡排序"""
for i in range(len(li) - 1): # 从0开始的第i趟
for j in range(len(li) - i - 1): # 要循环的趟数
if li[j] > li[j + 1]: # 后一个数比当前数大,就交换位置
# if li[j] < li[j+1]: # 降序排序, 大于是升序排序
li[j], li[j + 1] = li[j + 1], li[j]
print('每一趟排序后的列表: ', li)
li = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
print('排序前的列表: ', li)
bubble_sort(li)
print('排序后的列表: ', li)
"""
排序前的列表: [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
每一趟排序后的列表: [3, 38, 5, 44, 15, 36, 26, 27, 2, 46, 4, 19, 47, 48, 50]
每一趟排序后的列表: [3, 5, 38, 15, 36, 26, 27, 2, 44, 4, 19, 46, 47, 48, 50]
每一趟排序后的列表: [3, 5, 15, 36, 26, 27, 2, 38, 4, 19, 44, 46, 47, 48, 50]
每一趟排序后的列表: [3, 5, 15, 26, 27, 2, 36, 4, 19, 38, 44, 46, 47, 48, 50]
每一趟排序后的列表: [3, 5, 15, 26, 2, 27, 4, 19, 36, 38, 44, 46, 47, 48, 50]
每一趟排序后的列表: [3, 5, 15, 2, 26, 4, 19, 27, 36, 38, 44, 46, 47, 48, 50]
每一趟排序后的列表: [3, 5, 2, 15, 4, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
每一趟排序后的列表: [3, 2, 5, 4, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
每一趟排序后的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
每一趟排序后的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
每一趟排序后的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
每一趟排序后的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
每一趟排序后的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
每一趟排序后的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
排序后的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
"""那冒泡的时间复杂度是多少呢?n是列表的长度,每次循环并没有使问题的规模减半,所以,冒泡排序的时间复杂度是O(n2)。
冒泡排序还有可以有优化的地方:如果冒泡排序中的一趟排序没有发生交换,则说明列表已经是有序的了,可以直接结束算法。
def bubble_sort(li):
""" 冒泡排序"""
for i in range(len(li) - 1): # 从0开始的第i趟
for j in range(len(li) - i - 1): # 要循环的趟数
exchange = False
if li[j] > li[j + 1]: # 后一个数比当前数大,就交换位置
# if li[j] < li[j+1]: # 降序排序, 大于是升序排序
li[j], li[j + 1] = li[j + 1], li[j]
exchange = True # 说明有交换,此时列表还需要进行排序
print('每一趟排序后的列表: ', li)
if not exchange: # 如果这一趟结束,没有发生还,说明列表已经有序,可以结束算法了
return
# 列表从2开始就是有序的了,意味着不用进行冒泡排序
li = [46, 50, 48, 47, 2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44]
print('排序前的列表: ', li)
bubble_sort(li)
print('排序后的列表: ', li)
"""
排序前的列表: [46, 50, 48, 47, 2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44]
每一趟排序后的列表: [46, 48, 47, 2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 50]
每一趟排序后的列表: [46, 47, 2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 48, 50]
每一趟排序后的列表: [46, 2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 47, 48, 50]
每一趟排序后的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
每一趟排序后的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
排序后的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
"""由上例可以看到,改进后的算法,减少了很多的循环。
如果列表本身就是有序的,那么只需要算法只需要执行一趟就行了,而原算法还是需要执行n-1趟:
def bubble_sort(li):
""" 冒泡排序"""
for i in range(len(li) - 1): # 从0开始的第i趟
for j in range(len(li) - i - 1): # 要循环的趟数
exchange = False
if li[j] > li[j + 1]: # 后一个数比当前数大,就交换位置
# if li[j] < li[j+1]: # 降序排序, 大于是升序排序
li[j], li[j + 1] = li[j + 1], li[j]
exchange = True # 说明有交换,此时列表还需要进行排序
print('每一趟排序后的列表: ', li)
if not exchange: # 如果这一趟结束,没有发生交换,说明列表已经有序,可以结束算法了
return
li = [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
print('排序前的列表: ', li)
bubble_sort(li)
print('排序后的列表: ', li)
"""
排序前的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
每一趟排序后的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
排序后的列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
"""使用冒泡解决top K的问题:现在有n个数(有序),设计算法得到前k大的数(k<n)。我们如何用冒泡解决呢?
因为冒泡的每趟都会找出一个最大值,利用这个规则设计一个降序排序的冒泡算法,然后前k大的值,就循环k趟即可,后续是否是有序的就不管了,而不是循环n-1趟了。
先来看降序冒泡算法怎么实现:
import random
def desc_bubble_sort(li):
""" 冒泡排序,降序版 """
for i in range(len(li) -1):
for j in range(len(li) - 1, i, -1): # 从右往左循环列表
if li[j] > li[j - 1]: # 如果当前元素比前一个元素大,就交换它们的位置
li[j], li[j - 1] = li[j - 1], li[j]
li = list(range(10))
random.shuffle(li)
print('before: ', li)
desc_bubble_sort(li)
print('after: ', li)
"""
before: [4, 3, 0, 9, 7, 1, 8, 2, 6, 5]
after: [9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
"""然后将上面的算法再改一下,因为我们只需要前k大的数,所以,只需要循环k趟,而用循环n-1趟。
import random
import copy
def desc_bubble_sort(li, k):
""" 冒泡排序,降序版 """
for i in range(len(li) -1):
for j in range(len(li) - 1, i, -1): # 从右往左循环列表
if li[j] > li[j - 1]: # 如果当前元素比前一个元素大,就交换它们的位置
li[j], li[j - 1] = li[j - 1], li[j]
return li[0:k]
def desc_bubble_sort_topk(li, k):
""" 冒泡排序,降序版 """
for i in range(k):
for j in range(len(li) - 1, i, -1): # 从右往左循环列表
if li[j] > li[j - 1]: # 如果当前元素比前一个元素大,就交换它们的位置
li[j], li[j - 1] = li[j - 1], li[j]
return li[0:k]
li = list(range(10))
k = 5
random.shuffle(li)
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
print(desc_bubble_sort(li1, k)) # [9, 8, 7, 6, 5]
print(desc_bubble_sort_topk(li2, k)) # [9, 8, 7, 6, 5]
print('li1 after: ', li1)
print('li2 after: ', li2)
"""
li1 after: [9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
li2 after: [9, 8, 7, 6, 5, 2, 4, 3, 1, 0]
"""来看下循环k趟和循环n-1趟的性能差距:
import time
import random
import copy
def cal_time(func):
def wrapper(*args, **kwargs):
start = time.time()
res = func(*args, **kwargs)
print('{} running: {}'.format(func.__name__, time.time() - start))
return res
return wrapper
@cal_time
def desc_bubble_sort(li, k):
""" 冒泡排序,降序版 """
for i in range(len(li) -1):
for j in range(len(li) - 1, i, -1): # 从右往左循环列表
if li[j] > li[j - 1]: # 如果当前元素比前一个元素大,就交换它们的位置
li[j], li[j - 1] = li[j - 1], li[j]
return li[0:k]
@cal_time
def desc_bubble_sort_topk(li, k):
""" 冒泡排序,降序版 """
for i in range(k):
for j in range(len(li) - 1, i, -1): # 从右往左循环列表
if li[j] > li[j - 1]: # 如果当前元素比前一个元素大,就交换它们的位置
li[j], li[j - 1] = li[j - 1], li[j]
return li[0:k]
li = list(range(10000))
k = 10
random.shuffle(li)
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
print(desc_bubble_sort(li1, k)) # [9, 8, 7, 6, 5]
print(desc_bubble_sort_topk(li2, k)) # [9, 8, 7, 6, 5]
"""
desc_bubble_sort running: 6.768330335617065
[9999, 9998, 9997, 9996, 9995, 9994, 9993, 9992, 9991, 9990]
desc_bubble_sort_topk running: 0.01976466178894043
[9999, 9998, 9997, 9996, 9995, 9994, 9993, 9992, 9991, 9990]
"""性能差距挺大的。
选择排序
选择排序的思路:
- 一趟选择出列表中最小的数,放到列表第一个位置,那第一个位置此时我们认为它是有序区,其余的是无序区。
- 下一趟排序,从列表无序取最小的数,放到有序区的第二个位置
- 以此类推....
算法的关键点:有序区和无序区以及无序区最小的位置。
为了便于理解,我们先写个简单版的选择排序。
思路是:
- 每趟从列表中选择出一个最小的数。
- 然后将这个最小的数追加到一个临时列表中。
- 再将这个最小的数从原列表中删除。
def select_sort_simple(li):
tmp_list = []
for i in range(len(li)): # 循环 i 趟
min_value = min(li)
tmp_list.append(min_value)
li.remove(min_value)
print('临时列表: {} 原列表: {}'.format(tmp_list, li))
return tmp_list
li = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
select_sort_simple(li)
"""
临时列表: [2] 原列表: [3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
临时列表: [2, 3] 原列表: [4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
临时列表: [2, 3, 4] 原列表: [5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
临时列表: [2, 3, 4, 5] 原列表: [15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
临时列表: [2, 3, 4, 5, 15] 原列表: [19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
临时列表: [2, 3, 4, 5, 15, 19] 原列表: [26, 27, 36, 38, 44, 46, 47, 48, 50]
临时列表: [2, 3, 4, 5, 15, 19, 26] 原列表: [27, 36, 38, 44, 46, 47, 48, 50]
临时列表: [2, 3, 4, 5, 15, 19, 26, 27] 原列表: [36, 38, 44, 46, 47, 48, 50]
临时列表: [2, 3, 4, 5, 15, 19, 26, 27, 36] 原列表: [38, 44, 46, 47, 48, 50]
临时列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38] 原列表: [44, 46, 47, 48, 50]
临时列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44] 原列表: [46, 47, 48, 50]
临时列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46] 原列表: [47, 48, 50]
临时列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47] 原列表: [48, 50]
临时列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48] 原列表: [50]
临时列表: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50] 原列表: []
"""上面的代码理解起来简单,但是性能却不佳:
- 排序时,需要临时列表,空间浪费。
- 算法中,用到了列表的min和remove,这两个方法的时间复杂度都是O(n),而且删除列表时,列表的元素还要挪动
- 所以,这个算法的复杂度是O(n2)
来写个稍微好点的排序算法,思路是不需要用到临时列表,那么问题来了,每一趟选出来的最小的数,放到哪?这里可以放到列表的第一个位置(也可以是最后一个位置),也就是循环一趟列表,找出最小的数,把它放到列表的首位,而首位的元素怎么办?没错,它俩交换位置就行了。所以,此时的列表,我们逻辑上可以把它分为两部分,有序区和无序区。还有个问题需要考虑,初始最小的数从哪里来?或者是这个初始最小值怎么选出来的?
看代码:
def select_sort(li):
for i in range(len(li)-1): # 第 i 趟,最后一个数没必要再取了,因为它是最大了,所以 len(li)-1
min_loc = i # 初始,我们默认下标为0的元素是最小的
for j in range(i+1, len(li)): # 循环无序区,从当前下标的下一位到列表的最后,目的是找出无序区最小的数
if li[j] < li[min_loc]: # 判断无序区内的当前数是否比li[min_loc]小
min_loc = j # 将小于li[min_loc]的元素下标赋值给min_loc
li[i], li[min_loc] = li[min_loc], li[i] # 一次循环就是一趟,最小的数,把这个数交换到有序区去
# print(li) # 执行过程
li = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
select_sort(li)
"""
[2, 44, 38, 5, 47, 15, 36, 26, 27, 3, 46, 4, 19, 50, 48]
[2, 3, 38, 5, 47, 15, 36, 26, 27, 44, 46, 4, 19, 50, 48]
[2, 3, 4, 5, 47, 15, 36, 26, 27, 44, 46, 38, 19, 50, 48]
[2, 3, 4, 5, 47, 15, 36, 26, 27, 44, 46, 38, 19, 50, 48]
[2, 3, 4, 5, 15, 47, 36, 26, 27, 44, 46, 38, 19, 50, 48]
[2, 3, 4, 5, 15, 19, 36, 26, 27, 44, 46, 38, 47, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 36, 27, 44, 46, 38, 47, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 44, 46, 38, 47, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 44, 46, 38, 47, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 46, 44, 47, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
"""这个算法的复杂度是:O(n2)。
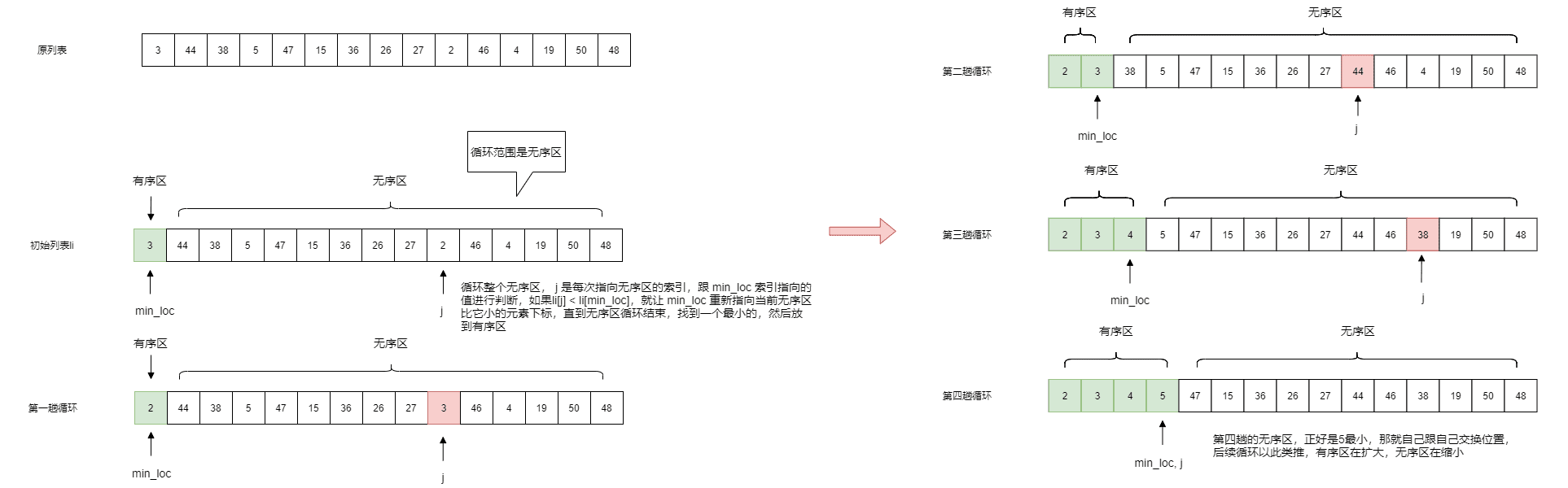
插入排序
插入排序的思想很简单,就像玩牌一样,比如手里有牌:
poker = [4, 10, 8]现在,摸到一张牌是5,那就要从右往左一个个对比,如果比5大,就把当前牌往右移动一个位置,直到找到一个比5小的元素3,然后将5插入4的后面;或者是找到列表的最左侧了,比如摸到一张牌是3,那再跟4比较,它比4小,4也往右挪,但此时3已经到了列表的最左侧了,这说明摸到3是最小,那就直接插入到列表的首位。

图片摘自:https://zhuanlan.zhihu.com/p/40695917
看代码:
def insert_sort(li):
""" 插入排序 """
for i in range(1, len(li)): # i表示摸到的牌的下标
tmp = li[i]
j = i - 1
while j >=0 and li[j] > tmp: # while循环就是从右向左找插入的位置
li[j+1] = li[j]
j -= 1
li[j+1] = tmp
# print(li, tmp)
li = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
insert_sort(li)
"""
[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 44
[3, 38, 44, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 38
[3, 5, 38, 44, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 5
[3, 5, 38, 44, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 47
[3, 5, 15, 38, 44, 47, 36, 26, 27, 2, 46, 4, 19, 50, 48] 15
[3, 5, 15, 36, 38, 44, 47, 26, 27, 2, 46, 4, 19, 50, 48] 36
[3, 5, 15, 26, 36, 38, 44, 47, 27, 2, 46, 4, 19, 50, 48] 26
[3, 5, 15, 26, 27, 36, 38, 44, 47, 2, 46, 4, 19, 50, 48] 27
[2, 3, 5, 15, 26, 27, 36, 38, 44, 47, 46, 4, 19, 50, 48] 2
[2, 3, 5, 15, 26, 27, 36, 38, 44, 46, 47, 4, 19, 50, 48] 46
[2, 3, 4, 5, 15, 26, 27, 36, 38, 44, 46, 47, 19, 50, 48] 4
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48] 19
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48] 50
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50] 48
"""插入排序的时间复杂度是:O(n2)
冒泡、选择和插入算法,它们三个的时间复杂度都是O(n2),排序效率不高,所以它们被称为low B 三人组。
所以,我们接下来,聊聊NB的排序算法。
快速排序
快速排序由 C. A. R. Hoare 在1962年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序算法步骤:
- 首先从列表中取出一个元素mid,这个mid可以是第一个元素,也可以是最后一个元素,也可以是随机一个元素。
- 使mid归位,在归为的过程中,列表被mid分为两部分,左边的都比mid小,右边的都比mid大。
- 递归完成排序。
快速排序框架:
def _quick_sort(li, left, right):
""" 快速排序 """
if left < right: # 递归结束条件,有两个及两个以上的元素,就继续递归
mid = partition(li, left, right) # mid: 在归为时,mid在列表中的下标
_quick_sort(li, left, mid-1) # 递归排序,mid左边的列表
_quick_sort(li, mid + 1, right) # 递归排序,mid右边的列表先来看partition函数怎么实现:
def partition(li, left, right):
""" 执行mid归位的过程 """
mid = li[left] # 将列表首位的元素作为mid
while left < right:
while left < right and li[right] >= mid: # mid右边的列表,从右往左找比mid小的数
right -= 1 # 从右往左挨个跟mid去判断
li[left] = li[right] # 从右往左找,找到一个比mid小的数,然后把它交换到mid左边去
print('⬅: ', li, "mid: ", mid)
while left < right and li[left] <= mid: # mid左边的列表,从左往右找,比mid大的数
left += 1 # 从左往右挨个跟mid去判断
li[right] = li[left] # 从左往右找,找到了一个比mid大的数,然后把它交换到mid右边去
print('➡: ', li, "mid: ", mid)
li[left] = mid # 把mid归位
print('mid归位: ', li)
return left # 用于后续分割列表,返回left和right都一样,因为二者相等
li = [5, 7, 4, 6, 3, 1, 2, 9, 8]
print('mid归位前的列表: ', li)
partition(li, 0, len(li) - 1)
print('mid归位后的列表: ', li)
"""
mid归位前的列表: [5, 7, 4, 6, 3, 1, 2, 9, 8]
⬅: [2, 7, 4, 6, 3, 1, 2, 9, 8] mid: 5
➡: [2, 7, 4, 6, 3, 1, 7, 9, 8] mid: 5
⬅: [2, 1, 4, 6, 3, 1, 7, 9, 8] mid: 5
➡: [2, 1, 4, 6, 3, 6, 7, 9, 8] mid: 5
⬅: [2, 1, 4, 3, 3, 6, 7, 9, 8] mid: 5
➡: [2, 1, 4, 3, 3, 6, 7, 9, 8] mid: 5
mid归位: [2, 1, 4, 3, 5, 6, 7, 9, 8]
mid归位后的列表: [2, 1, 4, 3, 5, 6, 7, 9, 8]
"""让partition函数和快速排序框架结合:
def partition(li, left, right):
""" 执行mid归位的过程 """
mid = li[left] # 将列表首位的元素作为mid
while left < right:
while left < right and li[right] >= mid: # mid右边的列表,从右往左找比mid小的数
right -= 1 # 从右往左挨个跟mid去判断
li[left] = li[right] # 从右往左找,找到一个比mid小的数,然后把它交换到mid左边去
print('⬅: ', li, "mid: ", mid)
while left < right and li[left] <= mid: # mid左边的列表,从左往右找,比mid大的数
left += 1 # 从左往右挨个跟mid去判断
li[right] = li[left] # 从左往右找,找到了一个比mid大的数,然后把它交换到mid右边去
print('➡: ', li, "mid: ", mid)
li[left] = mid # 把mid归位
print('mid归位: ', li)
return left # 用于后续分割列表,返回left和right都一样,因为二者相等
def _quick_sort(li, left, right):
""" 快速排序 """
if left < right:
mid = partition(li, left, right) # mid: 在归位时,mid在列表中的下标
_quick_sort(li, left, mid - 1) # 递归排序,mid左边的列表
_quick_sort(li, mid + 1, right) # 递归排序,mid右边的列表
li = [5, 7, 4, 6, 3, 1, 2, 9, 8]
print('before: ', li)
_quick_sort(li, 0, len(li) - 1)
print('after: ', li)
"""
before: [5, 7, 4, 6, 3, 1, 2, 9, 8]
⬅: [2, 7, 4, 6, 3, 1, 2, 9, 8] mid: 5
➡: [2, 7, 4, 6, 3, 1, 7, 9, 8] mid: 5
⬅: [2, 1, 4, 6, 3, 1, 7, 9, 8] mid: 5
➡: [2, 1, 4, 6, 3, 6, 7, 9, 8] mid: 5
⬅: [2, 1, 4, 3, 3, 6, 7, 9, 8] mid: 5
➡: [2, 1, 4, 3, 3, 6, 7, 9, 8] mid: 5
mid归位: [2, 1, 4, 3, 5, 6, 7, 9, 8]
⬅: [1, 1, 4, 3, 5, 6, 7, 9, 8] mid: 2
➡: [1, 1, 4, 3, 5, 6, 7, 9, 8] mid: 2
mid归位: [1, 2, 4, 3, 5, 6, 7, 9, 8]
⬅: [1, 2, 3, 3, 5, 6, 7, 9, 8] mid: 4
➡: [1, 2, 3, 3, 5, 6, 7, 9, 8] mid: 4
mid归位: [1, 2, 3, 4, 5, 6, 7, 9, 8]
⬅: [1, 2, 3, 4, 5, 6, 7, 9, 8] mid: 6
➡: [1, 2, 3, 4, 5, 6, 7, 9, 8] mid: 6
mid归位: [1, 2, 3, 4, 5, 6, 7, 9, 8]
⬅: [1, 2, 3, 4, 5, 6, 7, 9, 8] mid: 7
➡: [1, 2, 3, 4, 5, 6, 7, 9, 8] mid: 7
mid归位: [1, 2, 3, 4, 5, 6, 7, 9, 8]
⬅: [1, 2, 3, 4, 5, 6, 7, 8, 8] mid: 9
➡: [1, 2, 3, 4, 5, 6, 7, 8, 8] mid: 9
mid归位: [1, 2, 3, 4, 5, 6, 7, 8, 9]
after: [1, 2, 3, 4, 5, 6, 7, 8, 9]
"""快速排序的时间复杂度是:O(nlogn)
快速排序的问题
快速排序的问题之一就是概算法有最坏情况,比如当列表是倒叙列表或者列表近似有序时:
# li = [9, 1, 2, 3, 4, 5, 6, 7, 8]
li = [9, 8, 7, 6, 5, 4, 3, 2, 1]
print('before: ', li)
_quick_sort(li, 0, len(li) - 1)
print('after: ', li)
""" 最坏情况就是,每次都只交换一次,如果列表长度为n,那么将要递归n-1次
before: [9, 8, 7, 6, 5, 4, 3, 2, 1]
⬅: [1, 8, 7, 6, 5, 4, 3, 2, 1] mid: 9
➡: [1, 8, 7, 6, 5, 4, 3, 2, 1] mid: 9
mid归位: [1, 8, 7, 6, 5, 4, 3, 2, 9]
⬅: [1, 8, 7, 6, 5, 4, 3, 2, 9] mid: 1
➡: [1, 8, 7, 6, 5, 4, 3, 2, 9] mid: 1
mid归位: [1, 8, 7, 6, 5, 4, 3, 2, 9]
⬅: [1, 2, 7, 6, 5, 4, 3, 2, 9] mid: 8
➡: [1, 2, 7, 6, 5, 4, 3, 2, 9] mid: 8
mid归位: [1, 2, 7, 6, 5, 4, 3, 8, 9]
⬅: [1, 2, 7, 6, 5, 4, 3, 8, 9] mid: 2
➡: [1, 2, 7, 6, 5, 4, 3, 8, 9] mid: 2
mid归位: [1, 2, 7, 6, 5, 4, 3, 8, 9]
⬅: [1, 2, 3, 6, 5, 4, 3, 8, 9] mid: 7
➡: [1, 2, 3, 6, 5, 4, 3, 8, 9] mid: 7
mid归位: [1, 2, 3, 6, 5, 4, 7, 8, 9]
⬅: [1, 2, 3, 6, 5, 4, 7, 8, 9] mid: 3
➡: [1, 2, 3, 6, 5, 4, 7, 8, 9] mid: 3
mid归位: [1, 2, 3, 6, 5, 4, 7, 8, 9]
⬅: [1, 2, 3, 4, 5, 4, 7, 8, 9] mid: 6
➡: [1, 2, 3, 4, 5, 4, 7, 8, 9] mid: 6
mid归位: [1, 2, 3, 4, 5, 6, 7, 8, 9]
⬅: [1, 2, 3, 4, 5, 6, 7, 8, 9] mid: 4
➡: [1, 2, 3, 4, 5, 6, 7, 8, 9] mid: 4
mid归位: [1, 2, 3, 4, 5, 6, 7, 8, 9]
after: [1, 2, 3, 4, 5, 6, 7, 8, 9]
"""这个时候,通过随机选取mid来解决上述问题:
import random
def partition(li, left, right):
""" 执行mid归位的过程:最坏情况优化 """
k = random.randrange(left, right) # 随机选出一个元素
li[k], li[left] = li[left], li[k] # 让该元素和首位的元素进行交换
mid = li[left] # 将列表首位的元素作为mid
while left < right:
while left < right and li[right] >= mid: # mid右边的列表,从右往左找比mid小的数
right -= 1 # 从右往左挨个跟mid去判断
li[left] = li[right] # 从右往左找,找到一个比mid小的数,然后把它交换到mid左边去
print('⬅: ', li, "mid: ", mid)
while left < right and li[left] <= mid: # mid左边的列表,从左往右找,比mid大的数
left += 1 # 从左往右挨个跟mid去判断
li[right] = li[left] # 从左往右找,找到了一个比mid大的数,然后把它交换到mid右边去
print('➡: ', li, "mid: ", mid)
li[left] = mid # 把mid归位
print('mid归位: ', li)
return left
def _quick_sort(li, left, right):
""" 快速排序 """
if left < right:
mid = partition(li, left, right) # mid: 在归位时,mid在列表中的下标
_quick_sort(li, left, mid - 1) # 递归排序,mid左边的列表
_quick_sort(li, mid + 1, right) # 递归排序,mid右边的列表
# li = [9, 8, 7, 6, 5, 4, 3, 2, 1]
li = [9, 1, 2, 3, 4, 5, 6, 7, 8]
print('before: ', li)
_quick_sort(li, 0, len(li) - 1)
print('after: ', li)
"""
before: [9, 1, 2, 3, 4, 5, 6, 7, 8]
⬅: [3, 1, 2, 3, 9, 5, 6, 7, 8] mid: 4
➡: [3, 1, 2, 3, 9, 5, 6, 7, 8] mid: 4
mid归位: [3, 1, 2, 4, 9, 5, 6, 7, 8]
⬅: [1, 3, 2, 4, 9, 5, 6, 7, 8] mid: 1
➡: [1, 3, 2, 4, 9, 5, 6, 7, 8] mid: 1
mid归位: [1, 3, 2, 4, 9, 5, 6, 7, 8]
⬅: [1, 2, 2, 4, 9, 5, 6, 7, 8] mid: 3
➡: [1, 2, 2, 4, 9, 5, 6, 7, 8] mid: 3
mid归位: [1, 2, 3, 4, 9, 5, 6, 7, 8]
⬅: [1, 2, 3, 4, 6, 5, 6, 9, 8] mid: 7
➡: [1, 2, 3, 4, 6, 5, 6, 9, 8] mid: 7
mid归位: [1, 2, 3, 4, 6, 5, 7, 9, 8]
⬅: [1, 2, 3, 4, 5, 5, 7, 9, 8] mid: 6
➡: [1, 2, 3, 4, 5, 5, 7, 9, 8] mid: 6
mid归位: [1, 2, 3, 4, 5, 6, 7, 9, 8]
⬅: [1, 2, 3, 4, 5, 6, 7, 8, 8] mid: 9
➡: [1, 2, 3, 4, 5, 6, 7, 8, 8] mid: 9
mid归位: [1, 2, 3, 4, 5, 6, 7, 8, 9]
after: [1, 2, 3, 4, 5, 6, 7, 8, 9]
"""采用随机值的方式能在很大程度上解决问题,但这并不是完全解决该问题,万一随机的数也是第一个或者最后一个元素呢?但这么做已经很好了,如果还有遇到较近的,那——换个排序算法怎么样?
递归深度的问题
当选择快速排序算法时,除了要考虑之前的最坏情况,我们还要考虑递归本身的问题,比如递归占用空间和递归深度的问题。
堆排序
树
树与二叉树
树是一种数据结构
树是一种可以递归定义的数据结构
树是由n个节点组成的集合:
- 如果n=0,那么这是一棵空树;
- 如果n>0,那存在1一个节点作为树的根节点,其他节点可以分为m个集合,每个集合又是一棵树。
二叉树
二叉树:度不超过2的树
每个节点最多有两个孩子节点
两个孩子节点被区分为左孩子节点和右孩子节点
满二叉树:一个二叉树,如果每一层的节点树都达到最大值,则这个二叉树就是满二叉树
完全二叉树:叶子节点只能出现再最下层和次下层,并且最下面一层的节点都集中再该层最左边的若然位置的二叉树。可能理解起来稍微麻烦,所以请参考下图来加深理解:
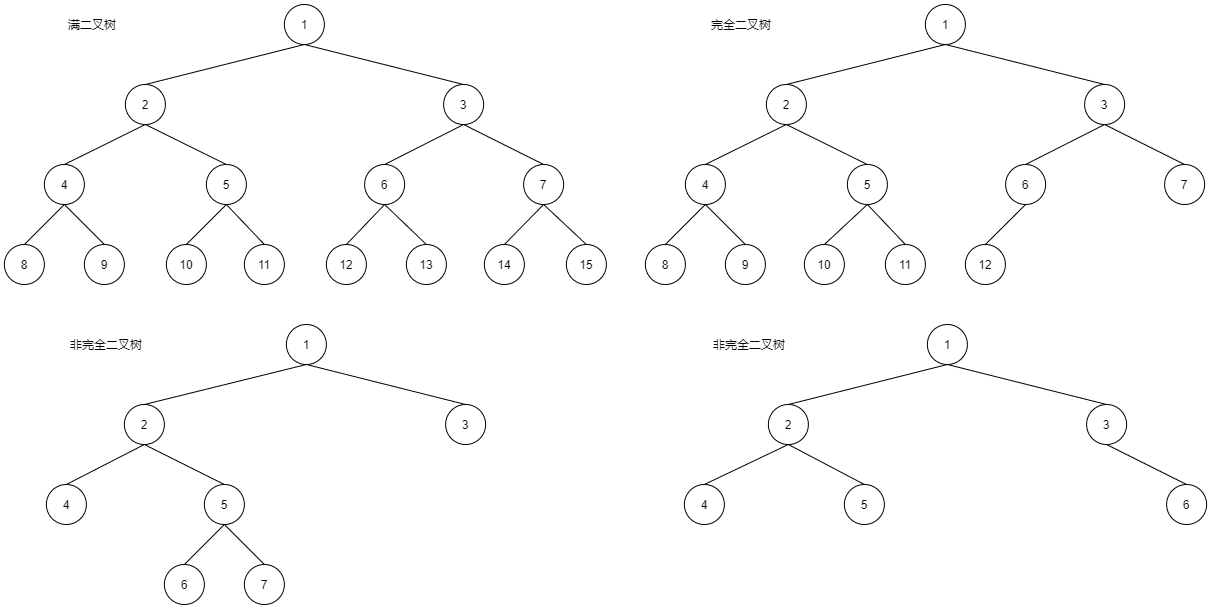
二叉树的存储方式:
- 链式存储
- 顺序存储
这里只简单探讨顺序存储方式,也就是用列表存储二叉树。
根据上图,我们来找出二叉树在列表中是怎么存储的。
父节点和左孩子节点的编号下标有什么关系?即怎么通过父节点找左孩子节点:
- 如果父节点在列表中的下标为
i,那么左孩子节点的下标计算公式是:2i+1,举个例子:- 二叉树中9和8的关系,父节点是9,它在列表中的下标是0,左孩子节点是8,下标是1,
2 * 0 + 1 = 1; - 二叉树中7和0的关系,父节点是7,它在列表中的下标是2,左孩子节点是0,下标是5,
2 * 2 + 1 = 5;
- 二叉树中9和8的关系,父节点是9,它在列表中的下标是0,左孩子节点是8,下标是1,
父节点和右孩子节点的编号下标有什么关系?即怎么通过父节点找右孩子节点:
- 如果父节点在列表中的下标为
i,那么右孩子节点的下标计算公式是:2i+2,举个例子:- 二叉树中9和7的关系,父节点是9,它在列表中的下标是0,右孩子节点是7,下标是2,
2 * 0 + 2 = 2; - 二叉树中7和1的关系,父节点是7,它在列表中的下标是2,右孩子节点是6,下标是6,
2 * 2 + 2 = 6;
- 二叉树中9和7的关系,父节点是9,它在列表中的下标是0,右孩子节点是7,下标是2,
问题来了,已知孩子节点的下标,怎么找它父亲的节点下标?假设孩子节点的下标设为i,那么它父亲的节点就是(i - 1) // 2,注意是整除2,这个公式无论左孩子找父亲还是右孩子找父亲,都适用。
- 先来个左孩子找父亲:
- 从2找6,2的下标为7,代入公式:
(7 - 1) // 2 = 3; - 从0找7,0的下标是5,代入公式:
(5 - 1) // 2 = 2;
- 从2找6,2的下标为7,代入公式:
- 右孩子找父亲:
- 从1找7,1的下标是6,代入公式:
(6 - 1) // 2 = 2; - 从5找8,5的下标是4,代入公式:
(4 - 1) // 2 = 1;
- 从1找7,1的下标是6,代入公式:
当然了,这里不是将树这种数据结构,所以就不过多展开了。
堆
堆!什么是堆
堆:一种特殊的完全二叉树结构,堆又可以分为大根堆和小根堆
- 大根堆:一棵完全二叉树,满足任一节点都比其孩子节点大
- 小根堆:一棵完全二叉树,满足任一节点都比其孩子节点小
接下来我们以大根堆展开,因为以大根堆排序的结果是升序的。
堆的向下调整性质
假设:节点的左右子树都是堆,但自身不是堆,可以通过一次向下调整来将其变换为一个堆。
如下图左侧根节点2,它不符合(大)堆的规定,因为它比左右子孩子都小,就需要调整,调整后的堆如下图右侧所示:
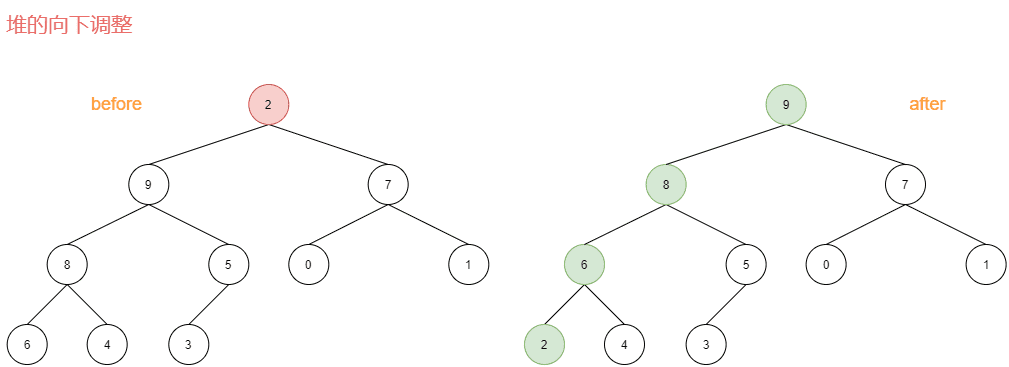
调整过程:
- 首先,2太小,无法"领导"9和7,所以先把2撸下来,然后从9和7中选个大的,9胜出。
- 9上位,2下到9的位置,问题来了,2还是太小,无法"领导"8和5,所以2又被撸下拉了,从8和5中选个大的,8胜出。
- 8上位,2下到8的位置,问题又来了,2还是太小,无法"领导"6和4,所以2又一次被撸下来了,从6和4中选个大的,6胜出。
- 6上位,2下到6的位置,这就好了,2"领导"它自己,此时堆是个合法的堆了,调整结束,否则还需要再次调整。
做了这么多的准备,重要要到了堆排序了。
堆排序
以大根堆展开
堆排序的过程
- 建立堆
- 得到堆顶元素,为最大元素
- 去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整重新使堆有序
- 堆顶元素为第二大元素
- 重复步骤3,直到堆为空
看起来一头雾水,其实,就是拿到一个待排序的无序列表,此时可以理解为这个无序列表就是堆,但它不是合法的堆,所以需要调整为合法的大根堆;由于大根堆的特性,堆顶的元素一定是最大值,然后将这个最大元素拿出来,但堆又不合法了,所以,再次调整堆使其合法,这样堆顶又最大了(其实是第二大,第一大已经拿出来了!),再拿出来,一番如此这般之后,堆空了,列表排序也完成了。我们称这个过程为"挨个出数"的过程。
说来简单,但也有个问题需要注意,挨个出数时,上面第三步中说,去掉堆顶,然后将堆的最后一个元素放到堆顶,为啥非要将堆的最后一个元素放到堆顶呢?来看图:
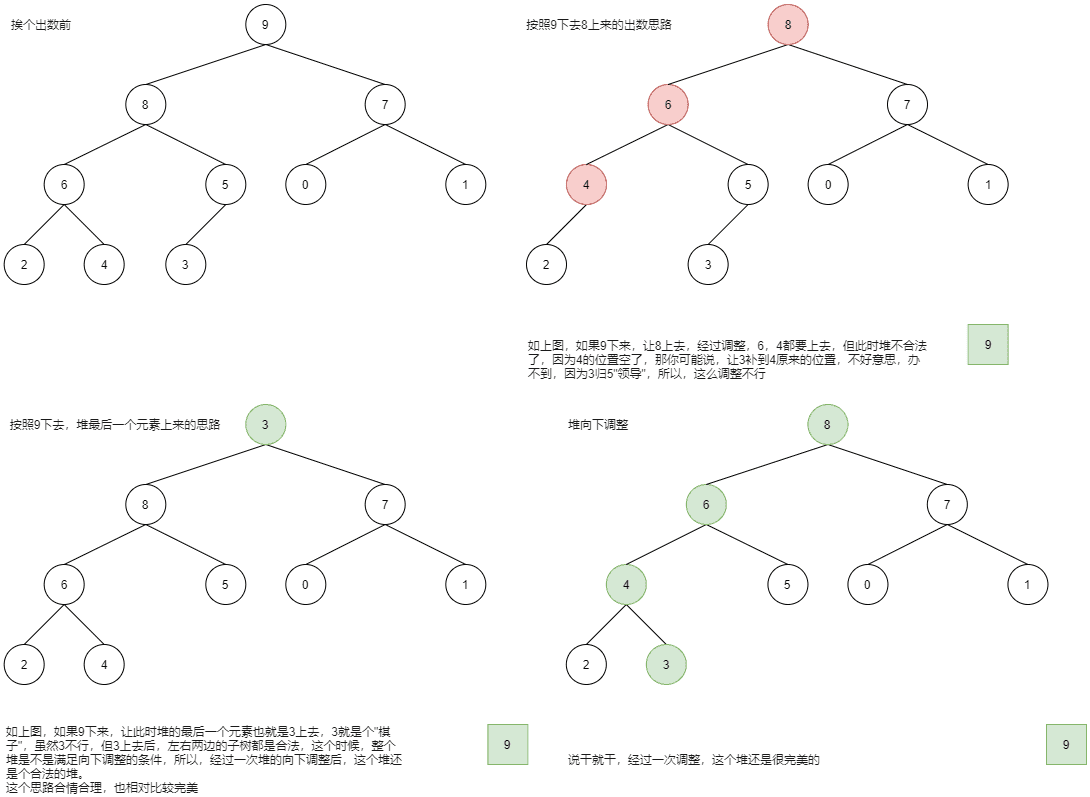
现在的问题来了,如何构造堆呢?
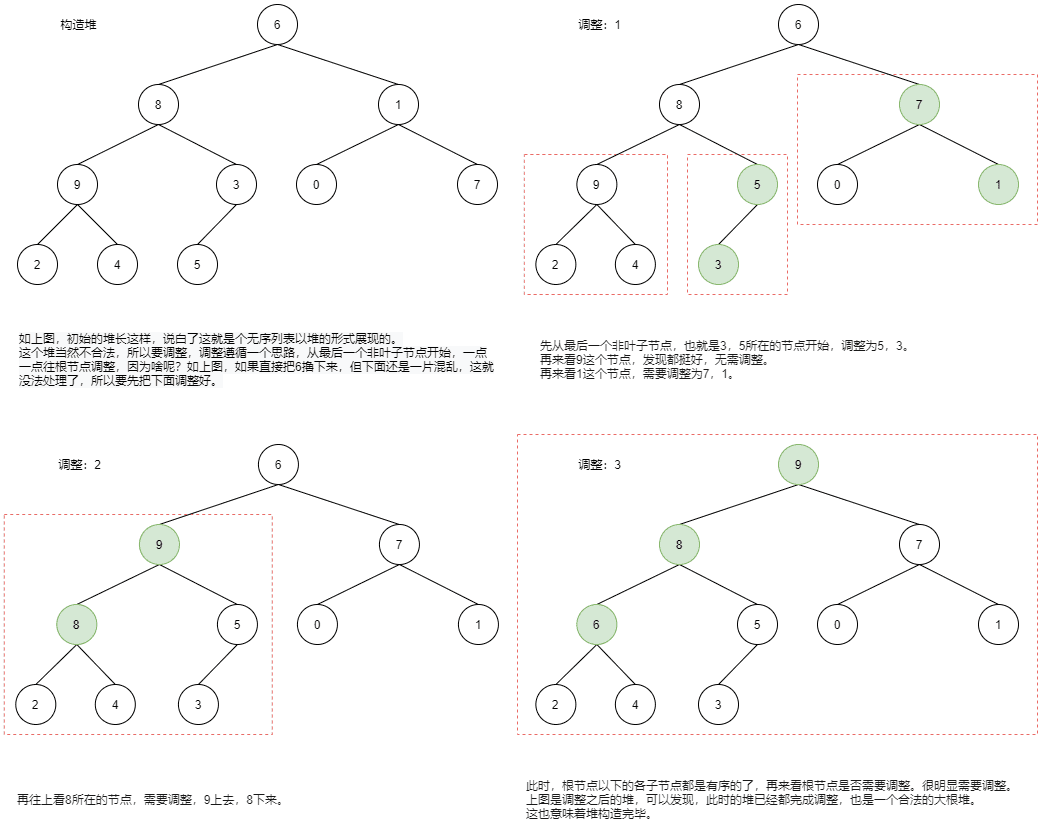
根据上图,我们来实现代码:
def sift(li, low, high):
"""
调整函数
:param li: 列表
:param low: 最开始指向的是堆顶,也就是根节点
:param high: 指向的堆的最后一个元素,作用就是判断son是否越界
:return:
"""
i = low # 最开始指向堆顶,而后续 i 随着循环在改变
son = 2 * i + 1 # 最开始指向左孩子,后续 son 也随着循环和判断在改变
tmp = li[low] # 把堆顶存起来,此时堆顶位置为空,即 i 位置为空
while son <= high: # 只要 son 位置有值,就需要对比和调整,否则意味着 i 的空位可以放 tmp 了
if son + 1 <= high and li[son + 1] > li[son]: # 如果右孩子存在,且该右孩子比左孩子大,就进行调整
son += 1 # son从原本的左孩子指向右孩子
# 经过上面if之后,son现在指向的是左右两个孩子中较大的那个孩子,接下来就是要看较大的孩子和tmp比,是否需要上去
if li[son] > tmp: # 如果孩子节点(左右孩子都有可能)比父节点大,儿子节点就向上调整,补上父节点的空位
li[i] = li[son] # 孩子节点补上父节点的空位,注意,此时的孩子节点空了
i = son # 将 i 再次指向空位节点,这个节点也成为了新的父节点
son = 2 * i + 1 # 孩子节点重新指向新的 i 节点的左孩子节点,如果i是最下层了,那么它没有下级节点了,那son指向的是一个不存在的位置,这个时候,直接跳出循环,将tmp写入i指向的空位就完了
else: # 如果孩子节点没有父节点大,退出循环,将临时存储起来的原堆顶补上 i 所在的空位
break
li[i] = tmp # 临时存储起来的原堆顶补上 i 所在的空位,无论怎么调整,最后都需要补空位,所以,放到了循环外面
print('li:', li, 'current heap top:', li[i], 'son:', son, 'tmp heap top:', tmp, 'high: ', high)
def heap_sort(li):
"""
堆排序:大根堆排序
构建堆,要注意的:
已知列表长度为 n,那列表的最后一个元素下标是 n - 1,同时这个下标也就是堆的最后一个元素下标
已知堆的最后一个元素的下标是 n - 1,求它的父节点的下标是?从孩子找父亲的公式是:(i - 1) // 2
现在知道了 i 是 n - 1,代入公式 (n - 1 - 1) // 2 整理后:(n - 2) // 2
也可以继续整理 n // 2 - 2 // 2 得 n // 2 - 1
n // 2 - 1 和 (n - 2) // 2 这两个公式你用哪个都行
最开始(n - 2) // 2 是最后一个非叶子节点的根节点,从这个节点开始,一点一点整理所有的子树,参考上图,即3、9、1、8、6这几个子树,都需要调整为大根堆,直到整个堆都是大根堆
"""
# 1. 构建堆
n = len(li)
for i in range((n - 2) // 2, -1, -1): # 倒着找 3 9 1 8 6这几个子树
# i 表示建堆时,要调整部分的下标,初始指向的堆的 3 这个节点,它需要和 5 调整
sift(li, low=i, high=n - 1) # high 永远指向堆的最后一个元素下标,它的作用就是判断son是否越界
li = [6, 8, 1, 9, 3, 0, 7, 2, 4, 5]
print('before: ', li)
heap_sort(li)
print('after: ', li)
"""
每次调整的i都代表是子树的根,也就是当前堆的堆顶;son大于high时,表示已处于最下层非叶子节点了,再往下就越界了
before: [6, 8, 1, 9, 3, 0, 7, 2, 4, 5]
li: [6, 8, 1, 9, 5, 0, 7, 2, 4, 3] current heap top: 3 son: 19 tmp heap top: 3 high: 9
li: [6, 8, 1, 9, 5, 0, 7, 2, 4, 3] current heap top: 9 son: 8 tmp heap top: 9 high: 9
li: [6, 8, 7, 9, 5, 0, 1, 2, 4, 3] current heap top: 1 son: 13 tmp heap top: 1 high: 9
li: [6, 9, 7, 8, 5, 0, 1, 2, 4, 3] current heap top: 8 son: 8 tmp heap top: 8 high: 9
li: [9, 8, 7, 6, 5, 0, 1, 2, 4, 3] current heap top: 6 son: 8 tmp heap top: 6 high: 9
after: [9, 8, 7, 6, 5, 0, 1, 2, 4, 3]
"""堆建完了,接下来是不是应该挨个出数了,参考下图理解出数的过程和调整过程:
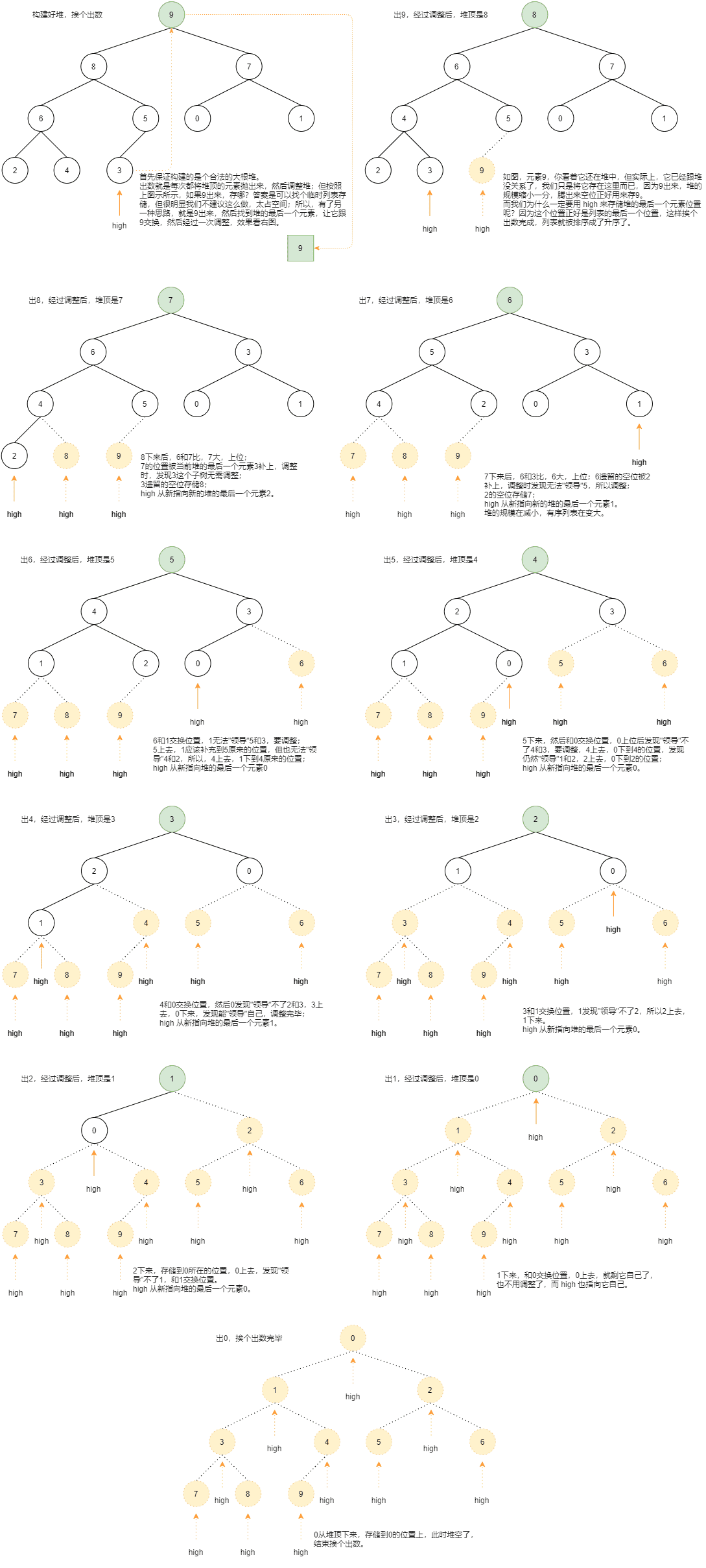
上代码:
def sift(li, low, high):
"""
调整函数
:param li: 列表
:param low: 最开始指向的是堆顶,也就是根节点
:param high: 指向的堆的最后一个元素,作用就是判断son是否越界
:return:
"""
i = low # 最开始指向堆顶,而后续 i 随着循环在改变
son = 2 * i + 1 # 最开始指向左孩子,后续 son 也随着循环和判断在改变
tmp = li[low] # 把堆顶存起来,此时堆顶位置为空,即 i 位置为空
while son <= high: # 只要 son 位置有值,就需要对比和调整,否则意味着 i 的空位可以放 tmp 了
if son + 1 <= high and li[son + 1] > li[son]: # 如果右孩子存在,且该右孩子比左孩子大,就进行调整
son += 1 # son从原本的左孩子指向右孩子
# 经过上面if之后,son现在指向的是左右两个孩子中较大的那个孩子,接下来就是要看较大的孩子和tmp比,是否需要上去
if li[son] > tmp: # 如果孩子节点(左右孩子都有可能)比父节点大,儿子节点就向上调整,补上父节点的空位
li[i] = li[son] # 孩子节点补上父节点的空位,注意,此时的孩子节点空了
i = son # 将 i 再次指向空位节点,这个节点也成为了新的父节点
son = 2 * i + 1 # 孩子节点重新指向新的 i 节点的左孩子节点,如果i是最下层了,那么它没有下级节点了,即son越界了
else: # 如果孩子节点没有父节点大,退出循环,将临时存储起来的原堆顶补上 i 所在的空位
break
li[i] = tmp # 临时存储起来的原堆顶补上 i 所在的空位,无论怎么调整,最后都需要补空位,所以,放到了循环外面
print('li:', li, 'current heap top:', li[i], 'son:', son, 'tmp heap top:', tmp, 'high: ', high)
def heap_sort(li):
"""
堆排序:大根堆排序
构建堆,要注意的:
已知列表长度为 n,那列表的最后一个元素下标是 n - 1,同时这个下标也就是堆的最后一个元素下标
已知堆的最后一个元素的下标是 n - 1,求它的父节点的下标是?从孩子找父亲的公式是:(i - 1) // 2
现在知道了 i 是 n - 1,代入公式 (n - 1 - 1) // 2 整理后:(n - 2) // 2
也可以继续整理 n // 2 - 2 // 2 得 n // 2 - 1
n // 2 - 1 和 (n - 2) // 2 这两个公式你用哪个都行
最开始(n - 2) // 2 是最后一个非叶子节点的根节点,从这个节点开始,一点一点整理所有的子树,参考上图,即3、9、1、8、6这几个子树,都需要调整为大根堆,直到整个堆都是大根堆
"""
# 1. 构建堆
n = len(li)
for i in range((n - 2) // 2, -1, -1): # 倒着找 3 9 1 8 6这几个子树
# i 表示建堆时,要调整部分的下标,初始指向的堆的 3 这个节点,它需要和 5 调整
sift(li, low=i, high=n - 1) # high 永远指向堆的最后一个元素下标,它的作用就是判断son是否越界
# 2. 挨个出数
"""
根据上图,先出9,跟最后一个元素3交换位置,然后9存储到3的位置,3到了堆顶,
但很明显3无法"领导"左右两棵子树(这两个子树都是合法的大根堆),需要做一次调整,
也不要忘了将 high 重新指向新的堆的最后一个元素
"""
for i in range(n - 1, -1, -1):
# i 指向当前堆的最后一个元素
li[0], li[i] = li[i], li[0] # 首先将9和3进行交换,紧接着就要进行调整了
sift(li, low=0, high=i - 1) # low:堆顶,因为每次要出的数都是堆顶,堆调整完了之后,要从新将high指向当前堆的最后一个元素,即之前i的前一个元素
# 原始列表
li = [6, 8, 1, 9, 3, 0, 7, 2, 4, 5]
print('before: ', li)
heap_sort(li)
print('after: ', li)
"""
before: [6, 8, 1, 9, 3, 0, 7, 2, 4, 5]
li: [6, 8, 1, 9, 5, 0, 7, 2, 4, 3] current heap top: 3 son: 19 tmp heap top: 3 high: 9
li: [6, 8, 1, 9, 5, 0, 7, 2, 4, 3] current heap top: 9 son: 8 tmp heap top: 9 high: 9
li: [6, 8, 7, 9, 5, 0, 1, 2, 4, 3] current heap top: 1 son: 13 tmp heap top: 1 high: 9
li: [6, 9, 7, 8, 5, 0, 1, 2, 4, 3] current heap top: 8 son: 8 tmp heap top: 8 high: 9
li: [9, 8, 7, 6, 5, 0, 1, 2, 4, 3] current heap top: 6 son: 8 tmp heap top: 6 high: 9
li: [8, 6, 7, 4, 5, 0, 1, 2, 3, 9] current heap top: 3 son: 17 tmp heap top: 3 high: 8
li: [7, 6, 3, 4, 5, 0, 1, 2, 8, 9] current heap top: 3 son: 6 tmp heap top: 3 high: 7
li: [6, 5, 3, 4, 2, 0, 1, 7, 8, 9] current heap top: 2 son: 9 tmp heap top: 2 high: 6
li: [5, 4, 3, 1, 2, 0, 6, 7, 8, 9] current heap top: 1 son: 7 tmp heap top: 1 high: 5
li: [4, 2, 3, 1, 0, 5, 6, 7, 8, 9] current heap top: 0 son: 9 tmp heap top: 0 high: 4
li: [3, 2, 0, 1, 4, 5, 6, 7, 8, 9] current heap top: 0 son: 5 tmp heap top: 0 high: 3
li: [2, 1, 0, 3, 4, 5, 6, 7, 8, 9] current heap top: 1 son: 3 tmp heap top: 1 high: 2
li: [1, 0, 2, 3, 4, 5, 6, 7, 8, 9] current heap top: 0 son: 3 tmp heap top: 0 high: 1
li: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] current heap top: 0 son: 1 tmp heap top: 0 high: 0
li: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] current heap top: 0 son: 1 tmp heap top: 0 high: -1
after: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
"""堆排序算法的时间复杂度是:
- sift循环每次减半,因为根节点有两个树杈,调整时要么走这边,要么走那边,所以是logn。
- 至于heap_sort:
- 第一个for循环是2分之n,sift是logn,总的就是nlogn
- 第二个for循环是n,里面的sift是logn,交换那个1可省略,总的就是nlogn
- 那整个堆排序的时间复杂度是:O(nlogn)
小根堆排序
小根堆排序可以使用Python内置的heapq模块来完成:
import heapq
li = [6, 8, 1, 9, 3, 0, 7, 2, 4, 5]
print("before: ", li)
# 构建堆,heapq模块构建的是小根堆
heapq.heapify(li) # 构建小根堆完毕
print('heap: ', li)
# 排序
tmp = range(len(li))
# heapq.heappop(li)每次都自动从小根堆中抛出堆顶元素,即最小的数,我们将这些数用列表收集起来,就得到了排序后的列表
new_list = [heapq.heappop(li) for i in tmp]
print('after: ', new_list)
"""
before: [6, 8, 1, 9, 3, 0, 7, 2, 4, 5]
heap: [0, 2, 1, 4, 3, 6, 7, 9, 8, 5]
after: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
"""手动实现小根堆
def small_sift(li, low, high):
"""
小根堆调整函数
:param li: 列表
:param low: 最开始指向的是堆顶,也就是根节点
:param high: 指向的堆的最后一个元素,作用就是判断son是否越界
:return:
"""
i = low # 最开始指向堆顶,而后续 i 随着循环在改变
son = 2 * i + 1 # 最开始指向左孩子,后续 son 也随着循环和判断在改变
tmp = li[low] # 把堆顶存起来,此时堆顶位置为空,即 i 位置为空
while son <= high: # 只要 son 位置有值,就需要对比和调整,否则意味着 i 的空位可以放 tmp 了
if son + 1 <= high and li[son + 1] < li[son]: # 如果右孩子存在,且该右孩子比左孩子小,就进行调整
son += 1 # son从原本的左孩子指向右孩子
# 经过上面if之后,son现在指向的是左右两个孩子中较大的那个孩子,接下来就是要看较大的孩子和tmp比,是否需要上去
if li[son] < tmp: # 如果孩子节点(左右孩子都有可能)比父节点小,儿子节点就向上调整,补上父节点的空位
li[i] = li[son] # 孩子节点补上父节点的空位,注意,此时的孩子节点空了
i = son # 将 i 再次指向空位节点,这个节点也成为了新的父节点
son = 2 * i + 1 # 孩子节点重新指向新的 i 节点的左孩子节点,如果i是最下层了,那么它没有下级节点了,即son越界了
else: # 如果孩子节点没有父节点大,退出循环,将临时存储起来的原堆顶补上 i 所在的空位
break
li[i] = tmp # 临时存储起来的原堆顶补上 i 所在的空位,无论怎么调整,最后都需要补空位,所以,放到了循环外面
print('li:', li, 'current heap top:', li[i], 'son:', son, 'tmp heap top:', tmp, 'high: ', high)
def small_heap_sort(li):
""" 小根堆排序算法 """
# 1. 构建小根堆
n = len(li)
for i in range((n - 2) // 2, -1, -1):
small_sift(li, low=i, high=n - 1)
# 2. 挨个出数
for i in range(n - 1, -1, -1):
li[0], li[i] = li[i], li[0]
small_sift(li, low=0, high=i - 1)
li = [6, 8, 1, 9, 3, 0, 7, 2, 4, 5]
print('before: ', li)
small_heap_sort(li)
print('after: ', li)
"""
before: [6, 8, 1, 9, 3, 0, 7, 2, 4, 5]
li: [6, 8, 1, 9, 3, 0, 7, 2, 4, 5] current heap top: 3 son: 9 tmp heap top: 3 high: 9
li: [6, 8, 1, 2, 3, 0, 7, 9, 4, 5] current heap top: 9 son: 15 tmp heap top: 9 high: 9
li: [6, 8, 0, 2, 3, 1, 7, 9, 4, 5] current heap top: 1 son: 11 tmp heap top: 1 high: 9
li: [6, 2, 0, 4, 3, 1, 7, 9, 8, 5] current heap top: 8 son: 17 tmp heap top: 8 high: 9
li: [0, 2, 1, 4, 3, 6, 7, 9, 8, 5] current heap top: 6 son: 11 tmp heap top: 6 high: 9
li: [1, 2, 5, 4, 3, 6, 7, 9, 8, 0] current heap top: 5 son: 5 tmp heap top: 5 high: 8
li: [2, 3, 5, 4, 8, 6, 7, 9, 1, 0] current heap top: 8 son: 9 tmp heap top: 8 high: 7
li: [3, 4, 5, 9, 8, 6, 7, 2, 1, 0] current heap top: 9 son: 7 tmp heap top: 9 high: 6
li: [4, 7, 5, 9, 8, 6, 3, 2, 1, 0] current heap top: 7 son: 4 tmp heap top: 7 high: 5
li: [5, 7, 6, 9, 8, 4, 3, 2, 1, 0] current heap top: 6 son: 5 tmp heap top: 6 high: 4
li: [6, 7, 8, 9, 5, 4, 3, 2, 1, 0] current heap top: 8 son: 5 tmp heap top: 8 high: 3
li: [7, 9, 8, 6, 5, 4, 3, 2, 1, 0] current heap top: 9 son: 3 tmp heap top: 9 high: 2
li: [8, 9, 7, 6, 5, 4, 3, 2, 1, 0] current heap top: 8 son: 1 tmp heap top: 8 high: 1
li: [9, 8, 7, 6, 5, 4, 3, 2, 1, 0] current heap top: 9 son: 1 tmp heap top: 9 high: 0
li: [9, 8, 7, 6, 5, 4, 3, 2, 1, 0] current heap top: 9 son: 1 tmp heap top: 9 high: -1
after: [9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
"""top k的问题
所谓top k的问题,其实就是各种排行榜问题,比如热搜榜、新歌榜.....
- 现在有n个数(有序),设计算法得到前k大的数(k<n),
- 解决思路:
- 排序后切片,时间复杂度是:O(nlogn)
- 使用Low B三人组,时间复杂度是:O(kn)
- 比如使用冒泡,因为冒泡排序每趟都会找到一个最大的数,那么前k大的数,就循环k趟就解决了,但问题也是存在的,如果n长度为1亿,那么要循环k趟.....也快不起来,时间复杂度是:O(kn)
- 插入排序
- 选择排序
- 堆排序,时间复杂度是:O(nlogk)
- 取列表前k个元素建立一个小根堆,堆顶就是目前第k大的数。
- 依次向后遍历原列表,对于列表中的元素,如果小于堆顶,则忽略该元素;如果大于堆顶,则将堆顶更换为该元素,并且对堆进行一次调整。
- 遍历列表所有元素后,倒叙弹出堆顶。
import time
import random
import copy
def cal_time(func):
def wrapper(*args, **kwargs):
start = time.time()
res = func(*args, **kwargs)
print('{} running: {}'.format(func.__name__, time.time() - start))
return res
return wrapper
def small_sift(li, low, high):
"""
小根堆调整函数
:param li: 列表
:param low: 最开始指向的是堆顶,也就是根节点
:param high: 指向的堆的最后一个元素,作用就是判断son是否越界
:return:
"""
i = low # 最开始指向堆顶,而后续 i 随着循环在改变
son = 2 * i + 1 # 最开始指向左孩子,后续 son 也随着循环和判断在改变
tmp = li[low] # 把堆顶存起来,此时堆顶位置为空,即 i 位置为空
while son <= high: # 只要 son 位置有值,就需要对比和调整,否则意味着 i 的空位可以放 tmp 了
if son + 1 <= high and li[son + 1] < li[son]: # 如果右孩子存在,且该右孩子比左孩子小,就进行调整
son += 1 # son从原本的左孩子指向右孩子
# 经过上面if之后,son现在指向的是左右两个孩子中较大的那个孩子,接下来就是要看较大的孩子和tmp比,是否需要上去
if li[son] < tmp: # 如果孩子节点(左右孩子都有可能)比父节点小,儿子节点就向上调整,补上父节点的空位
li[i] = li[son] # 孩子节点补上父节点的空位,注意,此时的孩子节点空了
i = son # 将 i 再次指向空位节点,这个节点也成为了新的父节点
son = 2 * i + 1 # 孩子节点重新指向新的 i 节点的左孩子节点,如果i是最下层了,那么它没有下级节点了,即son越界了
else: # 如果孩子节点没有父节点大,退出循环,将临时存储起来的原堆顶补上 i 所在的空位
break
li[i] = tmp # 临时存储起来的原堆顶补上 i 所在的空位,无论怎么调整,最后都需要补空位,所以,放到了循环外面
@cal_time
def heap_topk(li, k):
"""
:param li: 列表n
:param k: k的长度
:return: 返回前k大的列表
"""
tmp_heap = li[0:k]
# 1. 建堆,建立小根堆
for i in range((k - 2) // 2, -1, -1):
small_sift(tmp_heap, i, k - 1)
# 2. 遍历整个列表,找出前k大的数
for i in range(k, len(li) - 1):
if li[i] > tmp_heap[0]: # 表示原列表中有值比堆顶大,就替换到堆顶,然后再调整
tmp_heap[0] = li[i]
small_sift(tmp_heap, 0, k - 1)
# 3. 挨个出数,小根堆此时就是所有符合条件的前k大的数
for i in range(k - 1, -1, -1):
tmp_heap[0], tmp_heap[i] = tmp_heap[i], tmp_heap[0]
small_sift(tmp_heap, 0, i - 1)
return tmp_heap
@cal_time
def bubble_sort_topk(li, k):
""" 冒泡排序解决top问题"""
for i in range(k): # 从0开始的第i趟
for j in range(len(li) - 1, i, -1): # 要循环的趟数
if li[j] > li[j - 1]:
li[j], li[j - 1] = li[j - 1], li[j]
return li[0:10]
li = list(range(1000000))
k = 10
random.shuffle(li)
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
print(bubble_sort_topk(li1, k)) # 从一百万个数中,找出前10大的数
print(heap_topk(li2, k)) # 从一百万个数中,找出前10大的数
"""
bubble_sort_topk running: 3.320267677307129
[999999, 999998, 999997, 999996, 999995, 999994, 999993, 999992, 999991, 999990]
heap_topk running: 0.14784574508666992
[999999, 999998, 999997, 999996, 999995, 999994, 999993, 999992, 999991, 999990]
"""归并排序
利用切片替换列表的元素
归并中用到了列表的切片的知识点,就在这里回顾下:
li = [8, 2, 1, 5, 9, 7, 3, 4, 6]
tmp_list = ['x', 'y', 'z']
# 需求,用 tmp_list 替换掉 li 中的 7 3 4 这三个元素
li[-4:-1] = tmp_list
print(li) # [8, 2, 1, 5, 9, 'x', 'y', 'z', 6]归并排序——归并,什么是归并?
假设现在的列表分为两段,且各自有序:
那么,将这部分列表合为一个有序列表的操作就叫做归并。看上图,理解起来是不是很简单,没错就是很简单,我们结合下图,把上面的合并过程用代码实现:
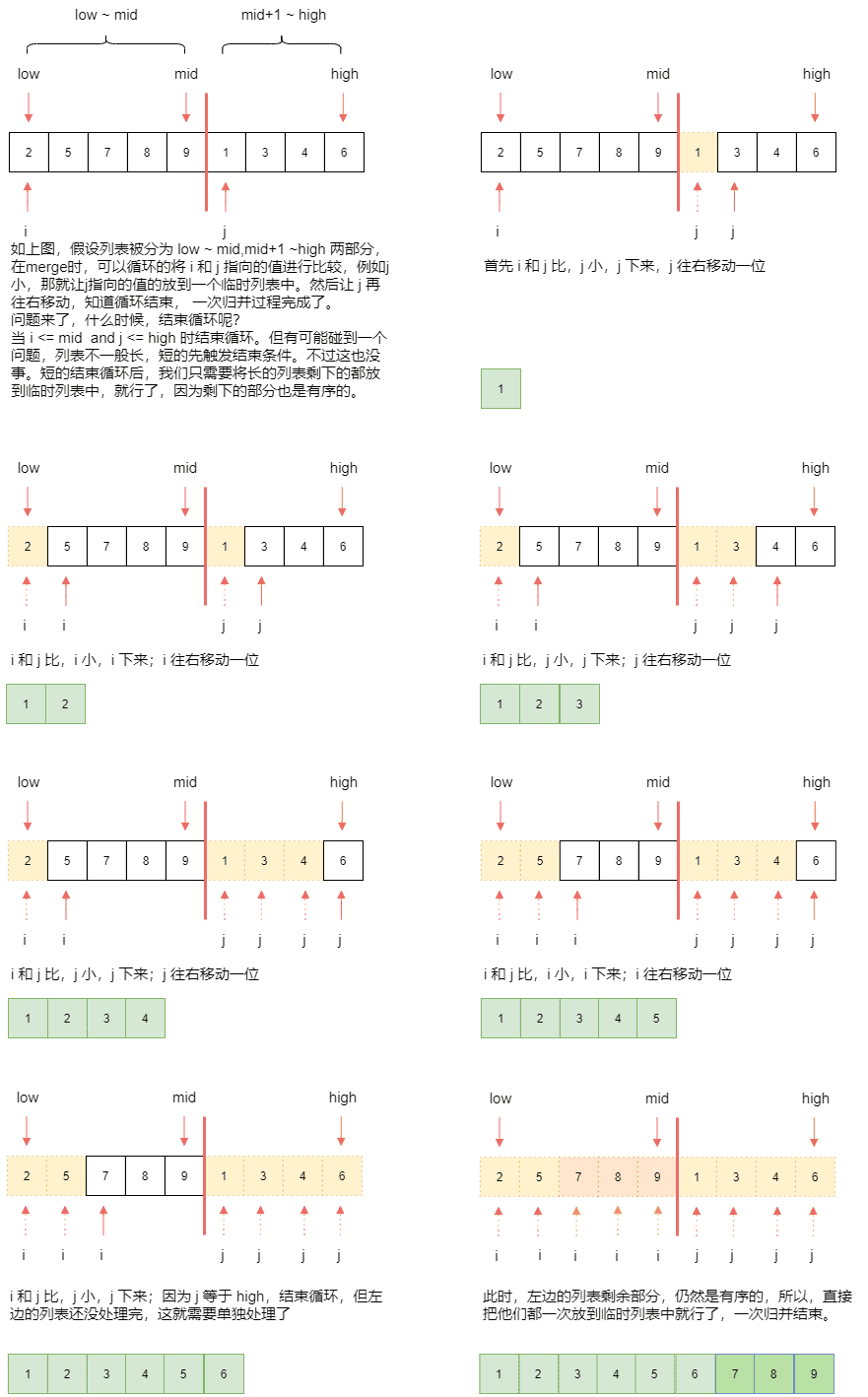
上代码:
def merge(li, low, mid, high):
"""
归并函数
:param li: 传过来的完成或者部分列表
:param low: 列表起始位置
:param high: 列表的结束位置
:param low ~ mid : 列表左半部分
:param mid+1 ~ high: 列表右半部分
:return:
"""
i = low # 初始的,让 i 等于列表的起始位置
j = mid + 1 # 列表右半部分的起始位置
tmp_list = [] # 临时列表,归并比大小时用到
while i <= mid and j <= high: # 左右两部分列表无论谁先结束,都退出循环
if li[i] < li[j]: # 如果左边i指向的元素比右边的小
tmp_list.append(li[i]) # 就把左边i指向的元素添加到临时列表中
i += 1 # 让i往往右移动一位
else: # 否则,就是右边的j指向的元素比左边i指向的元素大
tmp_list.append(li[j]) # 就把右边j指向的元素添加到临时列表中
j += 1 # 让j往右移动一位
# 当上面的循环结束后,两部分列表肯定有一边先结束,那另一边的列表剩余的元素需要手动添加到临时列表中
# 问题来了,哪边先结束呢?这里选择分别看一下
while i <= mid: # 如果左边的列表还有值,就依次添加到临时列表中
tmp_list.append(li[i])
i += 1
while j <= high: # 如果右边的列表还有值,就依次添加到临时列表中
tmp_list.append(li[j])
j += 1
# 左右两边都出数完成了,需要将临时列表写入到原来的列表中
# 临时列表是个有序列表,而原列表是无序列表,让临时列表中的元素替换到原列表中的元素
# 替换后,传过来的原列表的部分元素是有序的了
li[low:high + 1] = tmp_list
li = [2, 5, 7, 8, 9, 1, 3, 4, 6]
merge(li, low=0, mid=(len(li) - 1) // 2, high=len(li) - 1)
print(li) # [1, 2, 3, 4, 5, 6, 7, 8, 9]PS:这段代码写起来真的很顺手,要是所有的算法写起来都这么顺手该多好?!!!!!
代码写起来虽然顺手,但存在的问题也要解决啊!那就是归并的前提条件,需要两部分有序的列表!这我们怎么搞?
这里就又用到了递归的思想了:
- 分解:将列表越分越小,直至分解成一个元素的列表,一个元素的列表总是有序的吧!
- 终止条件:一个元素是有序的。
- 合并:将两个有序列表归并,这样列表的有序部分越来越多,递归完成,列表排序完毕。
参考下图理解:
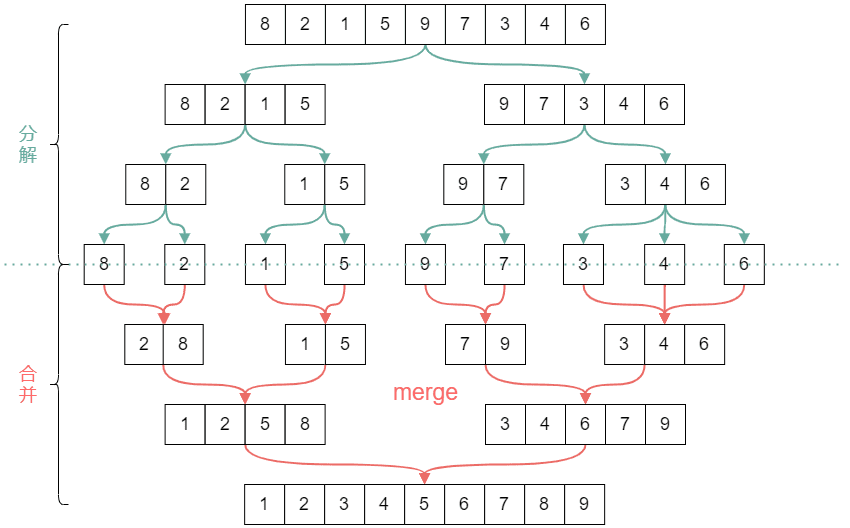
上代码:
def merge(li, low, mid, high):
"""
归并函数
:param li: 传过来的完成或者部分列表
:param low: 列表起始位置
:param high: 列表的结束位置
:param low ~ mid : 列表左半部分
:param mid+1 ~ high: 列表右半部分
:return:
"""
i = low # 初始的,让 i 等于列表的起始位置
j = mid + 1 # 列表右半部分的起始位置
tmp_list = [] # 临时列表,归并比大小时用到
while i <= mid and j <= high: # 左右两部分列表无论谁先结束,都退出循环
if li[i] < li[j]: # 如果左边i指向的元素比右边的小
tmp_list.append(li[i]) # 就把左边i指向的元素添加到临时列表中
i += 1 # 让i往往右移动一位
else: # 否则,就是右边的j指向的元素比左边i指向的元素大
tmp_list.append(li[j]) # 就把右边j指向的元素添加到临时列表中
j += 1 # 让j往右移动一位
# 当上面的循环结束后,两部分列表肯定有一边先结束,那另一边的列表剩余的元素需要手动添加到临时列表中
# 问题来了,哪边先结束呢?这里选择分别看一下
while i <= mid: # 如果左边的列表还有值,就依次添加到临时列表中
tmp_list.append(li[i])
i += 1
while j <= high: # 如果右边的列表还有值,就依次添加到临时列表中
tmp_list.append(li[j])
j += 1
# 左右两边都出数完成了,需要将临时列表写入到原来的列表中
# 临时列表是个有序列表,而原列表是无序列表,让临时列表中的元素替换到原列表中的元素
# 替换后,传过来的原列表的部分元素是有序的了
li[low:high + 1] = tmp_list
def merge_sort(li, low, high):
""" 归并排序 """
if low < high: # 至少有两个元素,就进行递归
mid = (low + high) // 2 # mid:把列表分两部分
merge_sort(li, low, mid) # 左半部分列表
merge_sort(li, mid + 1, high) # 右半部分列表
merge(li, low, mid, high) # 将左右两边的列表进行归并
li = [8, 2, 1, 5, 9, 7, 3, 4, 6]
print('before: ', li)
merge_sort(li, 0, len(li) -1)
print('after: ', li)
"""
before: [8, 2, 1, 5, 9, 7, 3, 4, 6]
after: [1, 2, 3, 4, 5, 6, 7, 8, 9]
"""归并排序的时间复杂度
- 一次归并是O(n)。
- 递归层数是多少呢?logn层。
- 所以,归并排序的复杂度:
- 时间复杂度:O(nlogn)。
- 空间复杂度:O(n),需要临时列表。
NB三人组小节
快排、堆排和归并排序的时间复杂度都是:O(nlogn)
一般情况下,就运行时间而言:快速排序 < 归并排序 < 堆排序
三种算法的优缺点:
- 快速排序:有最坏情况,该情况下算法效率底。
- 归并排序:需要额外的内存开销,就那个临时列表。
- 堆排序:在快的排序算法中,相对较慢。
希尔排序
趁着没往下看,赶紧回顾下插入排序算法吧!!!!
希尔排序(shell sort)是一种分组插入排序算法。
思路:
- 首先,取一个整数d1=n/2,将元素分为d1个组,每组相邻两个元素之间的距离是d1,在各组内进行直接插入排序。
- 取第二个整数d2=d1/2,重复上述分组排序过程,直到di=1,即所有元素都在同一组内进行直接插入排序。
希尔排序的每趟并不使某些元素有序,而是使整体数据越来越接近有序;最后一趟排序使所有的数有序。
其过程如下图所示:
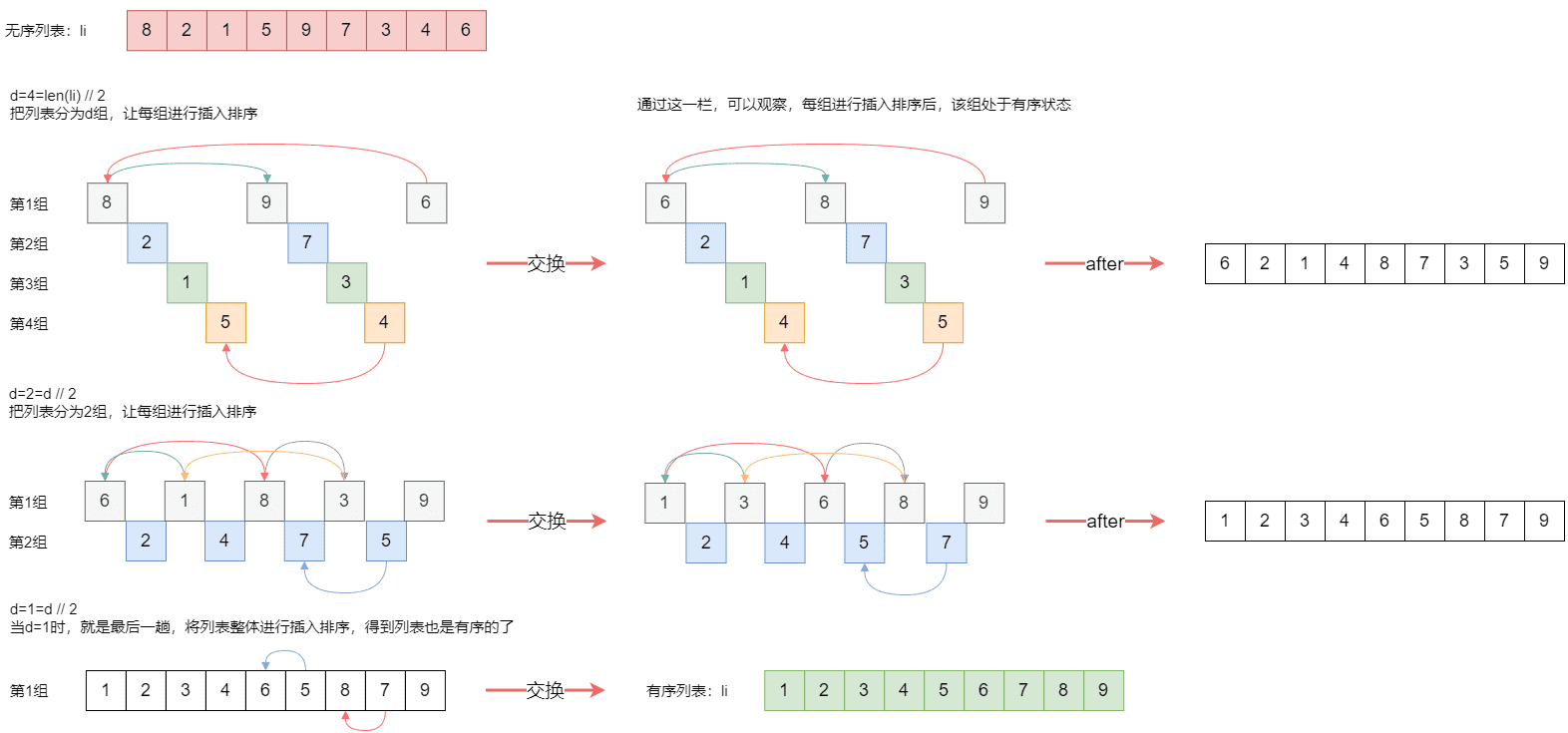
上代码:
def insert_sort_gap(li, gap):
""" 插入排序 - 希尔版 """
for i in range(gap, len(li)): # i表示摸到的牌的下标
tmp = li[i]
j = i - gap
while j >=0 and li[j] > tmp: # while循环就是从右向左找插入的位置
li[j+gap] = li[j]
j -= gap
li[j+gap] = tmp
def shell_sort(li):
""" 希尔排序 """
d = len(li) // 2
while d >= 1:
insert_sort_gap(li, gap=d)
d = d // 2
li = [8, 2, 1, 5, 9, 7, 3, 4, 6]
print('before: ', li)
shell_sort(li)
print('after: ', li)
"""
before: [8, 2, 1, 5, 9, 7, 3, 4, 6]
after: [1, 2, 3, 4, 5, 6, 7, 8, 9]
"""但希尔排序算法的性能不高!也就比Low B三人组高点。我们来做个对比:
li = list(range(100000))
random.shuffle(li)
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
li3 = copy.deepcopy(li)
insert_sort(li1)
shell_sort(li2)
heap_sort(li3)
"""
li = list(range(10000))
insert_sort running: 3.434455633163452
shell_sort running: 0.03989815711975098
heap_sort running: 0.03191423416137695
li = list(range(100000))
insert_sort running: 359.0289192199707
shell_sort running: 0.7031188011169434
heap_sort running: 0.4667818546295166
"""由结果可以看到,插入排序非常慢!希尔排序好了很多,但是跟NB三人组中最慢的堆排逼着还是慢了点。
那希尔排序的时间复杂度到底是多少呢?由于d的计算方式不同,希尔排序有各种不同的时间复杂度,有兴趣的可以自行查阅维基百科。
- 最好:O(n1.3)
- 最坏:O(n2)
- 平均:O(nlogn)~O(n2)
来自:https://zhuanlan.zhihu.com/p/107402632
以上这么多的算法,都属于比较排序,如果a比b大,然后怎样怎样....通过数学可以证明,比较排序算法,最快也是O(nlogn)。
我们在来研究下其他类型排序算法。
计数排序
对列表进行排序,已知列表中的数范围都在0到100之间,设计时间复杂度O(n)的算法。
这个算法相对好理解也很好写。
看图:

上代码:
import random
def count_sort(li, max_value=10):
"""
计数排序
:param li: 待排序列表
:param max_value: 待排序列表中最大的数
:return:
"""
tmp_list = [0 for _ in range(max_value + 1)] # 如果最大的数是100的话,所以要+1
for value in li:
# 每个下标存储对应值出现的次数,如下标0存储0在列表中出现的次数
tmp_list[value] += 1 # 如果对应下表是0,表示该元素没有在列表中出现过,如元素 2
# print(tmp_list) # [2, 4, 0, 2, 3, 3, 3, 1, 0, 1, 1]
li.clear() # 节省空间,再将排序结果写回到原列表
for index, value in enumerate(tmp_list):
# value记录的是index的个数,如index=0;value=2,表示0在列表中出现过2次,写2个0到li就行了
for i in range(value): # 出现几次 append 几次就完了,0次的话for循环不执行
li.append(index)
# li = [random.randint(0, 10) for _ in range(20)]
# print(li)
li = [1, 1, 4, 1, 0, 4, 1, 4, 5, 7, 3, 6, 5, 9, 3, 6, 10, 5, 0, 6]
print('before:', li)
count_sort(li, max_value=10)
print('after:', li)
"""
before: [1, 1, 4, 1, 0, 4, 1, 4, 5, 7, 3, 6, 5, 9, 3, 6, 10, 5, 0, 6]
after: [0, 0, 1, 1, 1, 1, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 7, 9, 10]
"""代码简单,但性能很高啊,我们来跟Python内置的算法比比啊:
import time
import random
import copy
def cal_time(func):
def wrapper(*args, **kwargs):
start = time.time()
res = func(*args, **kwargs)
print('{} running: {}'.format(func.__name__, time.time() - start))
return res
return wrapper
@cal_time
def list_builtin_sort(li):
""" 列表内置的sort方法 """
li.sort()
@cal_time
def count_sort(li, max_value=10):
tmp_list = [0 for _ in range(max_value + 1)]
for value in li:
tmp_list[value] += 1
li.clear()
for index, value in enumerate(tmp_list):
for i in range(value):
li.append(index)
max_value = 100
li = [random.randint(0, max_value) for _ in range(10000000)]
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
count_sort(li1, max_value=max_value)
list_builtin_sort(li2)
"""
# Python3.6
count_sort running: 1.4821240901947021
list_builtin_sort running: 1.8745102882385254
# Python3.9
count_sort running: 1.5681896209716797
list_builtin_sort running: 0.9401049613952637
"""是不是很有意思?我开始使用的是Python3.6的解释器,发现我们写的计数排序算法要比Python内置的列表的sort算法性能高!可喜可贺!!你(list.sort)虽然是C写的,我用Python写的,但我的算法比你好啊,所以我快!!!但快不过三秒!我用Python3.9解释器又跑了一下代码.....mmp,我开原称你为最强......
先来看计数算法的时间复杂度是多少?count_sort中,有两个大的for循环,他们整体上都分别循环一次列表,所以都是O(n)。虽然第二个for循环还嵌套了个for循环,但这个两个for循环也就是生成了一个列表,它跟上面的的for循环没啥区别,所以,计数算法的时间复杂度是:O(n)
虽然计数排序算法的性能也还可以,但这个算法的缺点也不少:
- 需要已知列表的元素大小范围,比如我们示例中,最大的元素是10或者100,也因此限制了该算法的应用场景。
- 该算法需要额外的内存空间,也就是临时列表,如果元素的范围是一个亿呢?就需要建立一个亿这么大的临时列表....
桶排序
在计数排序中,如果元素的范围比较大(比如在1到1亿之间),如何改造算法使其更优呢?
这里来介绍计数排序的优化算法——桶排序(Bucket Sort)。
桶排序的思路是:
- 首先将元素分布在不同的桶中。
- 再对每个桶中的元素进行排序。
看图理解:
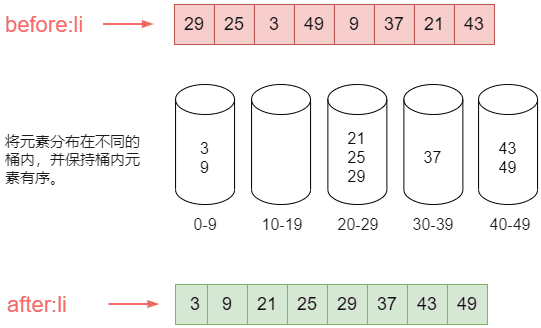
上代码:
def bucket_sort(li, n=5, max_num=50):
"""
桶排序
:param li: 待排序列表
:param n: 桶的个数
:param max_num: li中元素最大值
:return:
"""
buckets = [[] for _ in range(n)] # 创建桶 [[桶1], [桶2], [桶3], [桶4], [桶5]...]
for value in li: # 取出元素添加到对应的桶内
# 关键点在于:value应该插到几号桶内,要算出来
i = min(value // (max_num // n), n - 1) # i是桶号,即value应该放到几号桶内
"""
max_num // n 每个桶存储的数的范围
一个桶放多少个数,按照当前示例来说,50 // 5 = 10,一个桶放10个数,范围: 0-9;10-19;20-29;30-39;40-49
value // (max_num // n)
从li中取出的元素,应该放到几号桶呢?
如3,3 // 10 = 0 ,即应该放到0号桶内
如43, 43 // 10 = 4,即应该放到4号桶内
min(value // (max_num // n), n-1) n=5,但列表下标从0开始,所以最后一个桶的下标是 n-1 = 4
考虑到万一有元素比max_num大怎么办?比如来个50,现在最后一个桶只存储40-49这个范围内的数,但现在value是50,怎么搞?
答案就是把它放到最后一个桶内,但具体怎么搞呢?
50 // 10 = 5 ,但现在最后一个桶的下标是4,所以用min(5, 4) = 4,所以,50应该放到4号桶内
通过一番复杂的计算之后,i的值,就是value应该存放的桶号
"""
buckets[i].append(value) # 把value放到对应的桶内
# 保持桶内元素有序:冒泡算法思想
# 从右到左进行一一对比,插入到对应的位置
# 如将 1 插入到: [0, 2, 4],先将1append到列表中[0, 2, 4, 1]
# 然后让1从右到左先跟4比,1小,交换位置,再跟2比,1小,交换,再跟0比,1大,就插入到0后面
for j in range(len(buckets[i]) - 1, 0, -1):
if buckets[i][j] < buckets[i][j - 1]: # 如果右边的比左边的小,就交换
buckets[i][j], buckets[i][j - 1] = buckets[i][j - 1], buckets[i][j]
else: # 右边的比左边的大,就插入到这里就行了
break
# 现在该将各桶中元素一一取出放到列表中了
# 法1
li.clear()
for bucket in buckets:
li.extend(bucket)
# 法2
# tmp_list = []
# for i in buckets:
# tmp_list.extend(i)
# return tmp_list
li = [29, 25, 3, 49, 9, 37, 21, 43]
print('before:', li)
bucket_sort(li, n=5, max_num=50)
print('after:', li)
"""
before: [29, 25, 3, 49, 9, 37, 21, 43]
after: [3, 9, 21, 25, 29, 37, 43, 49]
"""来看看和计数排序算法哪个快:
max_value = 10000
max_li = 100000
bucket_num = 100
li = [random.randint(0, max_value) for _ in range(max_li)]
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
count_sort(li1, max_value=max_value)
bucket_sort(li2, n=bucket_num, max_num=max_value)
"""
len(li) = 100000
max_value = 10000
bucket_num=100
count_sort running: 0.01595783233642578
bucket_sort running: 8.888909578323364
"""没错,你没看错,数的范围最大值是一万,列表长度是10万,分配100个桶,结果.......说好的桶排是计数排序算法的优化版呢?负优化吧!!!
咳咳,上面那个示例,虽然姿势正确,但一看就不是老司机。经过测试,我发现桶的数量越多,性能越高:
"""
len(li) = 100000
max_value = 10000
bucket_num = 100
count_sort running: 0.01595783233642578
bucket_sort running: 8.888909578323364
len(li) = 100000
max_value = 10000
bucket_num = 1000
count_sort running: 0.015957355499267578
bucket_sort running: 0.7689692974090576
len(li) = 100000
max_value = 10000
bucket_num = 10000
count_sort running: 0.017950773239135742
bucket_sort running: 0.06984591484069824
max_value = 10000
max_li = 1000000
bucket_num = 10000
count_sort running: 0.13862895965576172
bucket_sort running: 0.740973711013794
max_value = 10000
max_li = 10000000
bucket_num = 10000
count_sort running: 1.8435328006744385
bucket_sort running: 7.941872835159302
"""我错了,我说错话了.....桶排序只有当桶的数量、列表长度、数的最大范围都在"合适"范围内,它比计数算法快多了!否则的话,性能反而极差。但怎么找"合适"的范围......你自己多尝试吧!我战略性放弃这个算法!本来这个算法就被人戏称"没什么人用"的算法,当然,也可能是我的姿势也不对!!!
额,还是有个点需要补充的,就是桶的数量最多只能小于等于列表元素的最大值,否则报错:
"""
代码中有一步是计算每个桶存储的数的范围的,也就是 max_num // n 的结果不能为0,因为这个值要作为被除数来计算出value应该
存放到几号桶内: value // (max_num // n),来个例子:
value = 10
max_num = 100
bucket_num分别等于99,100,101
100 // 99 = 1 --> 10 // 1 = 10
100 // 100 = 1 --> 10 // 1 = 10
100 // 101 = 0 --> 10 // 0 报错ZeroDivisionError: integer division or modulo by zero
"""桶排序——讨论
桶排序的表现取决于数据的分布,也就是需要对不同的数据排序时采取不同的分桶策略。
桶排序的时间复杂度:
- 平均情况时间复杂度:O(n+k),k是啥?说来话长啊,k是根据n和m算出来的。那m是啥?
- n:列表的长度。
- m:桶的个数。
- k:``logm * logn`,了解即可。
- 最坏情况时间复杂度:O(n2k)
空间复杂度:O(nk),这里的k是桶的长度。
最后,没有坏的算法,只有......
基数排序
基数排序的思路也很简单,举个例:有个员工表,根据年龄进行排序,年龄相同的根据薪资进行排序,这种多关键字的排序形式。 如,现在有列表li = [32, 13, 94, 52, 17, 54, 93],要对这个列表使用基数排序算法排序,那么套路是:
- 先比较各自的个位数,然后放到对应的桶中。
- 从桶中再依次取出根据个位数排序后的列表得到:
li = [32, 52, 13, 93, 94, 54, 17]。 - 再根据十位数值放入对应的桶中。
- 再从桶中依次取出,放入列表中,得到
li = [13, 17, 32, 52, 54, 93, 94]。 - 现在这个列表就是有序的了。
下图展示了上面的相关过程:
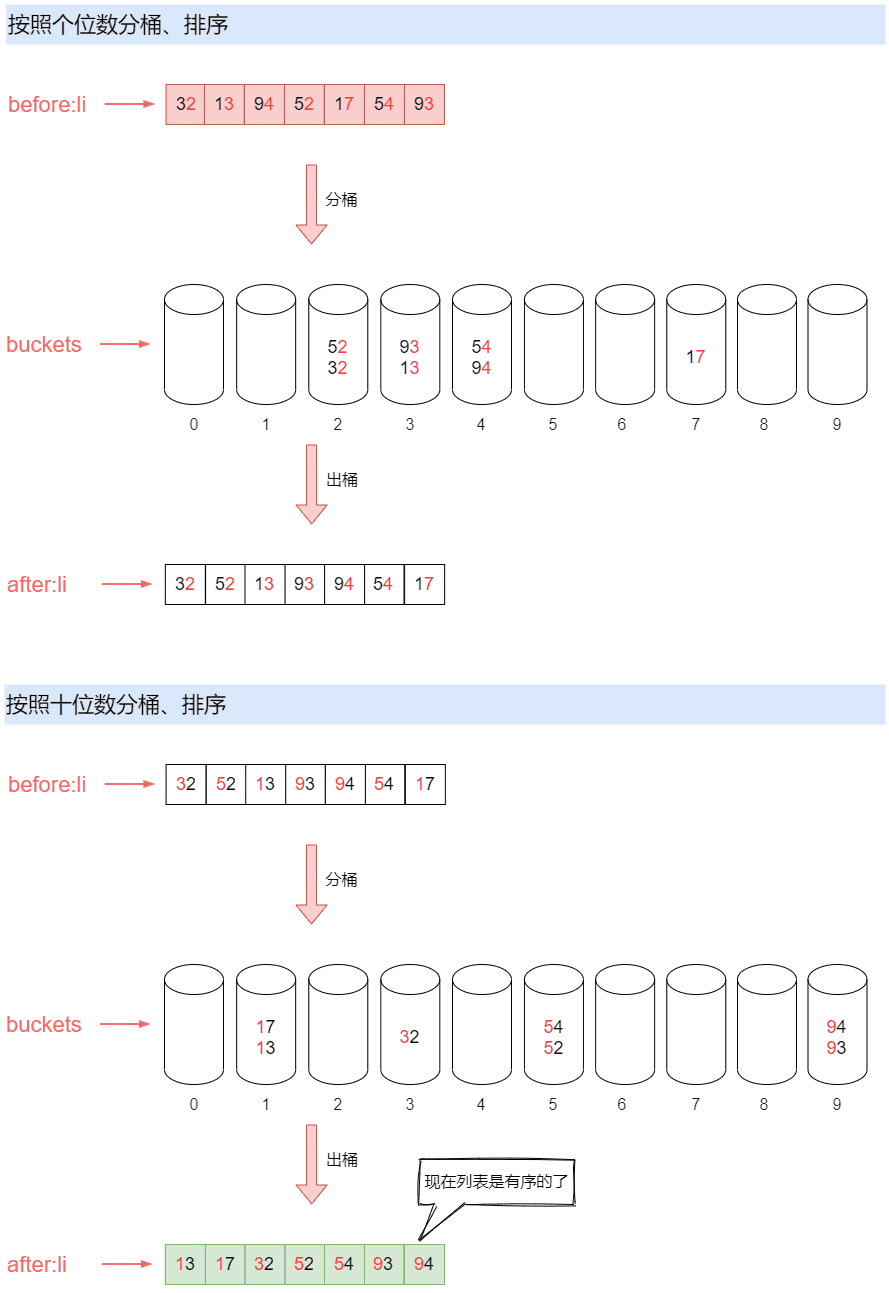
上代码:
def radix_sort(li, bucket_num=10):
""" 基数排序 """
max_num = max(li)
k = 0 # 根据 max_num 决定要入桶的次数,如 max_num 是3位数,就要循环3次: 0 1 2
while 10 ** k <= max_num: # 10 ** 0 = 1; 10 ** 1 = 10; 10 ** 2 = 100; 10 ** 3 = 1000 ......
# 1. 创建桶
buckets = [[] for _ in range(bucket_num)]
# 2. 分桶
for value in li: # 循环取值,根据当前位数进行将数写入到对应的桶中
"""
关键点在于如何从一个数中提取对应的位数,比如 987
第一次循环应该提取7;第二次提取8;第三次提取9,这个要用什么算出来
value 10 k
(987 // 10 ** 0) % 10 = 7
(987 // 10 ** 1) % 10 = 8
(987 // 10 ** 2) % 10 = 9
"""
i = (value // 10 ** k) % 10
buckets[i].append(value)
# 3. 从桶中取数,写回到原列表,3步执行完,表示根据当前位数排序完成
li.clear()
for bucket in buckets:
li.extend(bucket)
k += 1
# print('current li:', li)
li = [32, 13, 94, 52, 17, 54, 93]
print('before:', li)
radix_sort(li)
print('after:', li)
"""
before: [32, 13, 94, 52, 17, 54, 93]
current li: [32, 52, 13, 93, 94, 54, 17]
current li: [13, 17, 32, 52, 54, 93, 94]
after: [13, 17, 32, 52, 54, 93, 94]
"""问题来了,如是一个是五位数和2位数怎么搞?可以把2位数右边补零,搞成五位数嘛。 来找个快排对比下性能:
max_num = 1000000000
max_li = 1000000
li = [random.randint(0, max_num) for _ in range(max_li)]
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
quick_sort(li1)
radix_sort(li2)
"""
max_num = 100
max_li = 10000
quick_sort running: 0.06781792640686035
radix_sort running: 0.00797891616821289
max_num = 1000
max_li = 100000
quick_sort running: 0.7205934524536133
radix_sort running: 0.1146547794342041
max_num = 10000 # 如果列表长度不变,但最大值一直增大,快排效率不变,但基数排序效率慢慢变差
max_li = 1000000
quick_sort running: 7.680208444595337
radix_sort running: 1.9288489818572998
max_num = 100000
max_li = 1000000
quick_sort running: 5.587107419967651
radix_sort running: 2.4923593997955322
max_num = 1000000
max_li = 1000000
quick_sort running: 4.991452217102051
radix_sort running: 3.2557990550994873
max_num = 10000000
max_li = 1000000
quick_sort running: 4.583150863647461
radix_sort running: 3.395606517791748
max_num = 1000000000
max_li = 1000000
quick_sort running: 5.269375562667847
radix_sort running: 4.496855974197388
"""可以看到,当列表最大元素越小,基数排序要比快排快,但如果列表长度不变,最大元素却越来越大,那基数排序慢慢的性能就下来了!这是怎么回事儿呢?这里就要从二者的时间复杂度来说了。
小结
基数排序的时间复杂度:O(kn),k表示while循环的次数,也就是最大的数字位数;n表示列表的长度。再来说基数排序为啥随着k变大,性能变差。
- 首先快排的时间复杂度是O(nlogn),
logn=log(2, n);而基数O(kn),k=log(10, n),结论是以10为底的对数比以2为底的对数小。 - 但如果基数排序的k越来越大.......而快排还是nlogn不变,所以,可不就慢了么。
基数排序的空间复杂度是O(k+n)。
基数排序的使用注意事项:
- 如果k值越大,则基数排序越慢,反之性能越高。
- 基数排序需要额外的内存空间,也就是要考虑桶的空间占用。
timsort
看完了各种排序算法,我想你也很好奇,list.sort内部使用的算法是什么吧!
timsort是Python内置的混合算法,它派生于归并排序和插入排序;是一种混合稳定的和自适应排序算法。
timsort的时间复杂度最好情况为O(n),平均情况为O(nlogn),最差情况为O(nlogn);空间复杂度为O(n)。
- https://github.com/python/cpython/blob/master/Objects/listsort.txt
- https://medium.com/@sivabalanb92/timsort-in-python-wickedly-fast-sorting-bc57bb46a030
- http://www.xefan.com/archives/83857.html
- https://blog.csdn.net/sinat_35678407/article/details/82974174
先写这么多,后面有时间再搞。
相关面试题
以上,我们聊了聊常用的经典的查找和排序算法。
你可以去leetcode去刷刷题练练手了,也可以参考下面的链接,我这里整理好了一份面试题。
参考:https://gitee.com/wangzhangkai/iq.git
see also: