最长公共子序列
这个最长公共子序列(LCS,longest common subsequence)的学习套路:
- 基本的概念了解,要了解什么是子序列、子序列的特点、它和子串有啥不同、什么是最长公共子序列。
- 总结规律,就是要思考LCS是否具有最优子结构性质,也就是是否能找出递推公式。
- 根据递推公式完成代码实现。
基本概念了解
子序列
一个序列的子序列是在该序列中删除若干元素后得到的序列,如"ABCD"和"BDF"都是"ABCDEFG"的子序列,这里子序列成立的条件:
- 得到的子序列和序列的顺序不能变,相对顺序要一致,可以不连续,例如"BDF"是"ABCDEFG"的子序列,只不是从序列中剔除了若干元素,但整体上子序列的顺序没有变;如果变了,就不是子序列了,比如把"BDF"的"F"放到前面得到"FBD",这个子序列就不成立了。
子序列和子串概念不一样
子序列和子串不一样概念不一样,子串必须是连续的,而子序列可以不连续,比如上例的"ABCD"是"ABCDEFG"的子串,但"BDF"却不是"ABCDEFG"的子串,因为"BDF"不连续。
最长公共子序列
最长公共子序列问题:给定两个序列X和Y,求X和Y长度最大的公共子序列。
- 例:X="ABBCBDE",Y="DBBCDB",LCS(X, Y)="BBCD"
空序列
空序列是任意序列的子序列,比如ABCD和EFG的最长公共子序列是空字符串,也既是空序列。
应用场景:字符串的相似度对比,模糊搜索,基因工程。
最优子结构性质
这一小节,其实就是聊怎么根据规律找出递推公式的这么一个过程,再根据递推公式求结果。
这部分可以根据表格实现,即根据表格,按照递推公式去填表。
递推公式
首先LCS需要用到二维数组,所以我们要特别的理解dp[i][j],那么什么是dp[i][j]呢?比如有两个字符串s1和s2,即s1[0→i]和s2[0→j]的LCS,就叫做dp[i][j]。
那么dp[i][j]怎么求呢?也就是如何推导出递推公式呢?
定理(LCS的最优子结构):令X={x1, x2, ..., xm}和Y={y1,y2, ..., yn}为两个序列(注意序号从1开始的),Z={z1, z2, ..., zk}为X和Y的任意LCS,其:
- 如果
xm=yn,则zk=xm=ym,且Zk=1是Xm-1和Yn-1的一个LCS。- 例如:对 X = "AGTGATG",Y = "GTTAG",则Z = "GTAG",此时m = 7,n = 5,k = 4(从1开始)。比较X和Y最后一位,x7 = y5,同时删去,Xm-1 = "AGTGAT",Yn-1 = "GTTA",Zk-1 = "GTA"。我们可以发现,Zk-1就是Xm-1和Yn-1的一个LCS。
- 如果
xm≠yn,那么zk≠xm意味着Z是Xm-1和Y的一个LCS。- 例如:对 X = "AGTGAT",Y = "GTTA",则Z = "GTA",此时m = 6,n = 4,k = 3(从1开始)。比较最后一位,x6 ≠ y4,z3 ≠ x6 ,Xm-1 = "AGTGA",Z是Xm-1和Yn的一个LCS。
- 如果xm≠yn,那么zk≠yn意味着Z是X和Yn-1的一个LCS。
- 例如,我们将上一个示例的X和Y互换,对 Y = "AGTGAT",X = "GTTA",则Z = "GTA",此时n = 6,m = 4,k = 3(从1开始)。比较最后一位,x4 ≠ y6,z3 ≠ x4 ,Yn-1 = "AGTGA",Z是Xm和Yn-1的一个LCS。
从上面的定理中,可以得出一个结论,再求X={x1, x2, ..., xm}和Y={y1,y2, ..., yn}的一个LCS时,我们需要解决两个问题:
- 如果xm=yn,我们应该求解xm-1和yn-1的一个LCS。
- 如果xm ≠ yn,我们必须求解两个子问题:xm-1和yn的一个LCS 和 xm和yn-1的一个LCS。两个较长者应该为xm和yn的一个LCS。
所以,最优解的递推式:
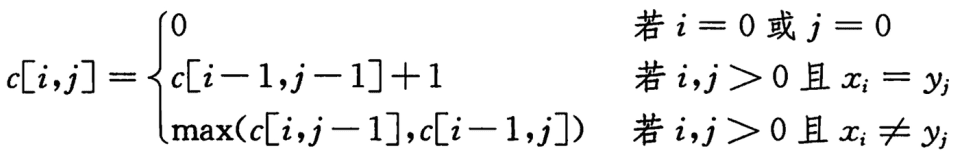
其c[i, j]表示Xi和Yj的LCS长度,i 和 j 可以认为两个串的长度,即X[0-i]和Y[0-j]。
PS:c[i, j]也可称之为dp[i, j]的。
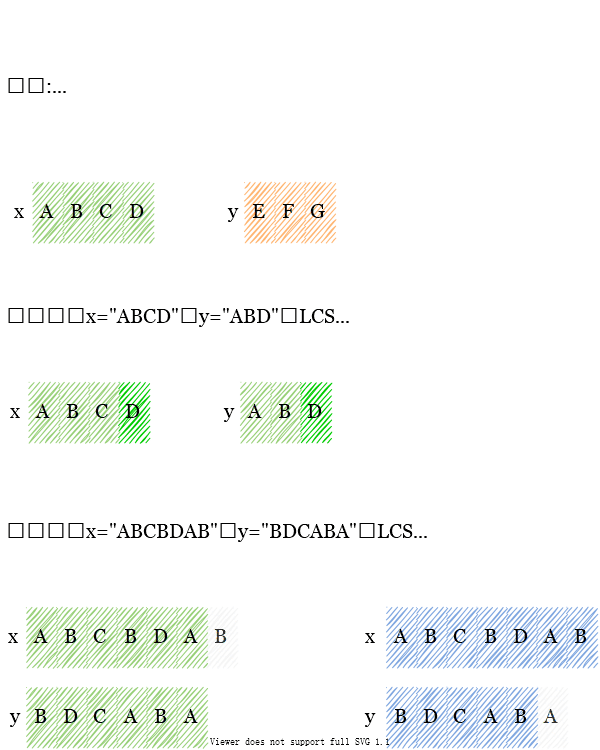
上面递推式的相应示例如下:
https://alchemist-al.com/algorithms/longest-common-subsequence
https://blog.csdn.net/sinat_40872274/article/details/87946808
包教包会