about
数据结构是指相互之间存在着一种或者多种关系的数据元素的集合和该集合中数据元素之间的关系组成。
简单来说,数据结构就是设计数据以何种方式组织并存储在计算机中。
N.Writh说:"程序=数据结构+算法"。
数据结构的分类
数据结构按照其逻辑结构可以分为线性结构、树结构、图结构。
- 线性结构:数据结构中的元素存在一对一的相互关系。
- 树结构:数据结构中的元素存在一对多的相互关系。
- 图结构:数据结构中的元素存在多对多的相互关系。
数组
通常在介绍Python的列表的时候,都会说:Python中的列表相当于别的语言中的数组...
但实际上Python中的列表和别的语言中的数组还是有些区别的,所以,我们单独的,简单来说下数组。
在C中,关于数组:
- 定义数组时,要指定数组的长度。
- 数组中的数据类型要一致。
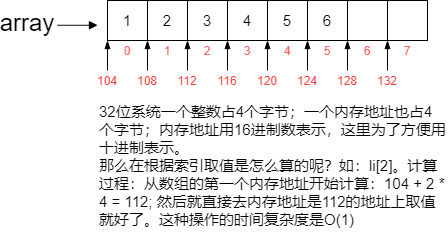
在内存中,这里以32位系统举例。
创建一个数组,在内存中会开辟一个块连续的内存空间。
列表
Python中的列表跟数组的区别有两点很明显的区别:
- 定义列表时,无需指定列表长度。
- 举个例子:如创建一个长度为3的列表,Python解释器会创建一个比3更长的列表,留有一定的冗余度,以便后续的添加操作。问题也有,如果一直添加,留的冗余空间也会用完,那再插入新的数据之前,Python会重新创建一个列表副本,然后再允许新的数据插入,这个新列表会预留更大的冗余空间,原列表会被垃圾回收机制回收。
- 列表中的数据类型不必一致,那这一点是怎么做到的呢?这是因为列表用的是引用语义进行存储,详情参考Python中变量的存储关系。
上图:
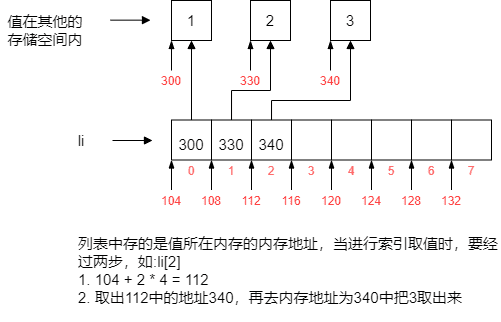
列表的删除和插入都是O(n)的操作,比如删除下标为0的元素,右面的元素都会往左移动。插入也类似,其他元素都要往后移动以腾出空位置进行插入操作。
栈
栈(Stack)是一个数据集合,可以理解为只能在一端进行插入或者删除操作的列表。
栈的特点:后进先出 LIFO(last-in,first-out)。
栈的相关概念:栈顶、栈底。
栈的基本操作:
- 进栈(压栈):push
- 出栈:pop
- 取栈顶:gettop,相当于看一眼栈顶的元素是啥,但我不拿走.....
创建栈
栈在Python中可以用列表实现:
class Stack(object):
def __init__(self):
self.stack = []
def push(self, element):
""" 入栈 """
self.stack.append(element)
def gettop(self):
""" 查栈顶元素 """
return self.stack[-1] if self.stack else None
def pop(self):
""" 出栈 """
return self.stack.pop() if self.stack else None
stack = Stack()
stack.push(1)
stack.push(2)
stack.push(3)
print(stack.pop()) # 3栈的应用——括号匹配问题
括号匹配问题:给一个字符串,其中包含小、中、大括号三种,求该字符串中的括号是否匹配。
例如:
(){}[]:匹配。([){}}:不匹配。(({[{(){}()[]}]})):匹配。
来看参考:
class Stack(object):
def __init__(self):
self.stack = []
def push(self, element):
""" 入栈 """
self.stack.append(element)
def gettop(self):
""" 查栈顶元素 """
return self.stack[-1] if self.stack else None
def pop(self):
""" 出栈 """
return self.stack.pop() if self.stack else None
def is_empty(self):
""" 如果栈为空,返回True """
return False if self.stack else True
def bracket_match(s):
stack = Stack()
match_dict = {"}": "{", "]": "[", ")": "("}
for ch in s:
# 如果不是括号就进入下一次循环
if ch not in list(match_dict.values()) + list(match_dict.keys()):
continue
if ch in match_dict.values(): # 如果是左括号
stack.push(ch)
else: # 否则 ch 就是右括号
if stack.is_empty(): # 只有右括号,少了左括号,表示匹配失败
return False
elif stack.gettop() == match_dict[ch]: # 如果栈顶和 ch 是一对,就出栈
stack.pop()
else: # 如果栈顶和 ch 不是一对,表示匹配失败
return False
# 最后如果栈为空,表示都匹配上了,否则就有匹配失败的
return True if stack.is_empty() else False
print(bracket_match("(){}[]")) # True
print(bracket_match("([){}}")) # False
print(bracket_match("(({[{(){}()[]}]}))")) # True
print(bracket_match("(2+3)/5*(3+2)")) # True
print(bracket_match("(2+3)/5*(3+2")) # False
print(bracket_match("2+3)/5*(3+2")) # False采用栈来解决迷宫问题,参考:https://www.cnblogs.com/Neeo/articles/9239450.html
队列
队列(Queue)是一个数据集合,仅允许在一端进行插入,另一端进行删除。
进行插入的一端称为队尾(rear),插入动作称为进队或者入队。
进行删除的一端称为队头(front),删除动作被称为出队。
队列的性质:先进先出(First-in,First-out)。
队列的实现方式——环形队列
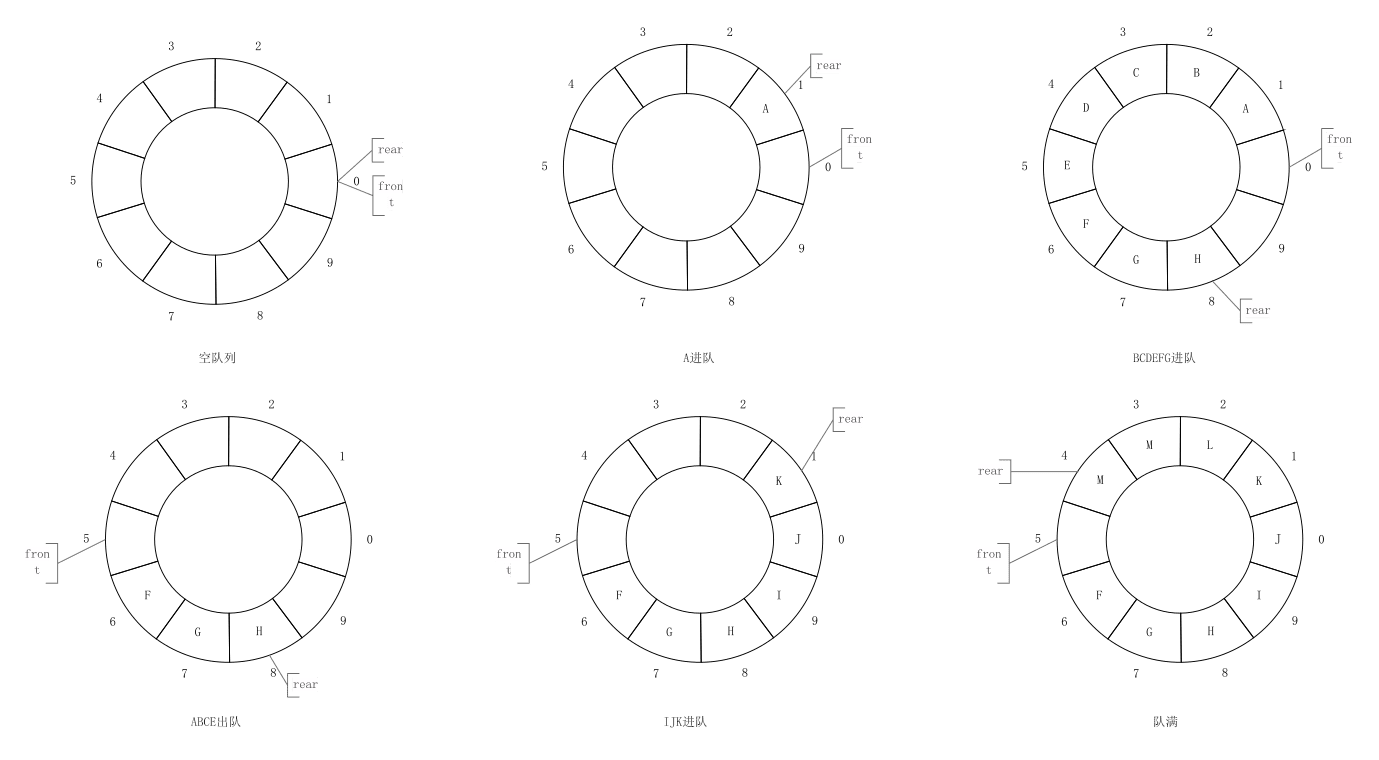
在上图中,演示了从一个空队列到队满的情况,这里面需要注意:
- 当队列为空时,rear等于front。
- 当队满时,观察图,发现还有留有一个空位,那为啥就说队满了呢?其原因,就是如果把那个空的位置也插入值,那rear等于front了,这个时候无法判断这个队列到底是空的还是满的,所以就留一个空位来标识队满。
- front永远指向空位。
- 还有一个重点,虽然看图是个环形,但首尾如何衔接?当插入到尾部后,下一次插入怎么就能插入到队首呢?怎么算出来的?也就是如图所示,怎么样让9+1=0?答案是取余运算:
(9 + 1) % 10 = 0。
在环形队列中,当队尾指针front等于环形队列长度减一时,再前进一个位置就自动到0。
- 队首指针前进1:front = (front+1) % maxsize
- 队尾指针前进1:rear = (rear + 1) % maxsize
- 队空条件:rear == front
- 队满条件:(rear + 1) % maxsize == front
手写一个简单队列:
class Queue(object):
def __init__(self, max_size=10):
# self.max_size = max_size + 1 # 因为队满时,有个空位,队列长度为10的话,只能存9个元素,所以,这里可以加1
self.max_size = max_size + 1
self.queue = [0 for _ in range(self.max_size)]
print(self.queue, len(self.queue))
self.rear = 0 # 队尾
self.front = 0 # 队首
def push(self, element):
""" 进队列 """
if self.is_filled(): # 如果队列已满
raise ValueError('queue is filled!')
else:
self.rear = (self.rear + 1) % self.max_size
self.queue[self.rear] = element
def pop(self):
""" 出队列 """
if self.is_empty(): # 如果队列为空
raise IndexError:("queue is empty!")
else:
self.front = (self.front + 1) % self.max_size
return self.queue[self.front] # 出队后,该位置元素没有删除,但我们不用管它,后续新的元素入队会覆盖它
def is_empty(self):
""" 判断队列是否为空 """
return self.rear == self.front
def is_filled(self):
""" 判断队列是否已满 """
return (self.rear + 1) % self.max_size == self.front
@property
def get_front(self):
""" 查看队首元素 """
if self.is_empty(): # 如果队列为空
raise IndexError:("queue is empty!")
else:
return self.queue[self.front]
@property
def get_rear(self):
""" 查看队尾元素 """
if self.is_empty(): # 如果队列为空
raise IndexError:("queue is empty!")
else:
return self.queue[self.rear]
q = Queue()
for i in range(10):
q.push(i)
print(q.get_front) # 0
print(q.get_rear) # 9双向队列
上面说的都是单向队列,其实队列还有一种队列:双向队列,也叫做双端队列,双向队列理解起来也很简单,就是两端都支持进出。
双向队列这里可以用Python内置模块实现:
from collections import deque
# 队列的创建
q = deque() # 创建一个空队列
"""
deque接收两个可选参数
deque(iterable, maxlen)
iterable: 为队列添加初始值
maxlen: 队列的长度
"""
# 这是个单向队列
q.append(1) # 从队尾添加元素
q.popleft() # 从队头出队
print(q.popleft()) # 1
# 双向队列
q.appendleft(2) # 从队头添加元素
q.pop() # 从队尾抛出元素注意,deque模块实现的队列有个特点,就是队满了后,再添加元素,会先从另一头抛出一个元素,然后执行添加,这点跟我们手写的队列有点不一样。
利用这个特点可以做点有意思的事儿,比如模拟实现Linux的tail -f 命令,即返回文件后几行:
from collections import deque
def tail(n):
with open('test.txt', 'r', encoding='utf-8') as f:
q = deque(f, n)
return [line.strip()for line in q]
print(tail(5))队列的应用
采用队列来解决迷宫问题,参考:https://www.cnblogs.com/Neeo/articles/9239450.html
链表
链表是由一系列节点组成的元素集合。
链表又分为:
- 单向链表。
- 双向链表。
- 环形链表。
线性表
无论是列表还是链表都可以抽象地称其为线性表。一个线性表是某类元素的集合,它还记录着元素之间的顺序关系,线性表是最基本的数据结构之一,应用十分广泛,根据其存储方式不同,又分为:
- 顺序表(列表),将元素顺序的存储在一块连续的存储空间中,元素间的顺序关系由它们的存储顺序自然表示。
- 链表,各个元素分布在不同的存储空间中,它们之间的关系通过"链"连起来。
单向链表
单向链表也叫做单链表,是链表中最简单的一种形式,它每个节点包含两部分:
- 数据域(item),也叫做信息域、元素域,存数据用的。
- 链接域,指向下一个节点的指针next,而最后一个节点的next指向一个空值。
通过节点间的相互连接,最终串联成一个链表。
链表通常有一个头节点,如下图的a1,通过头节点可以找到后续的任意节点。当然,你也可以称an为尾节点。
class Node(object):
""" 节点 """
def __init__(self, item):
self.item = item # 元素
self.next = None # 初始节点的next为None
class SingleNode:
""" 单链表的节点 """
def __init__(self, item):
self.item = item # 元素
self.next = None # 初始节点的next为None链表的操作
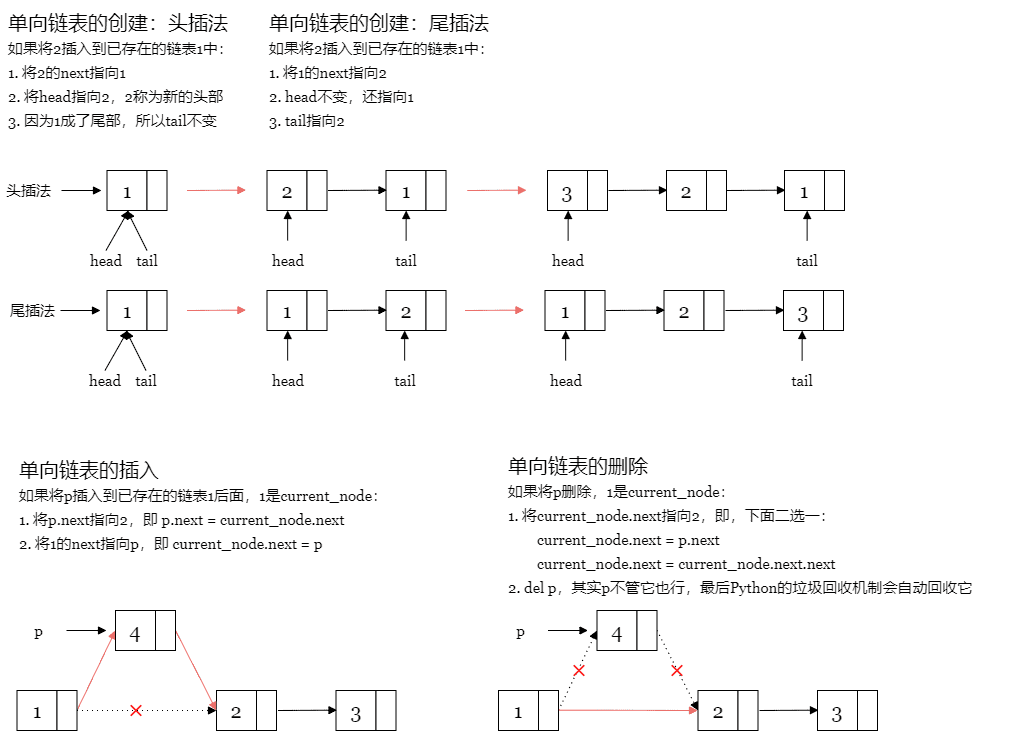
创建链表有两种方法:
- 头插法。
- 尾插法。
顾名思义,一个从头插入,一个从尾部插入。
class Node:
def __init__(self, item):
self.item = item
self.next = None # 初始节点的next节点为None
class OperatorLinkList(object):
""" 单向链表的操作 """
def create_link_list_head(self, li):
""" 头插法,这里可以不管tail,因为tail一直不变 """
head = Node(li[0]) # 将列表下标为0的元素当作head
for element in li[1:]: # 因为下标为0的元素已经被当作头节点了,所以这里从下标1开始循环
node = Node(element) # 创建新的节点
node.next = head # 将新节点的next指向上个节点
head = node # 然后将head指向新节点
return head # 返回链表的head,可以通过head找到链表中的所有节点
def create_link_list_tail(self, li):
""" 尾插法,这里可以不管head,因为head一直不变 """
head = Node(li[0]) # 将列表下标为0的元素当作head
tail = head # 刚开始,尾巴和head都指向头节点
for element in li[1:]:
node = Node(element) # 创建新的节点
tail.next = node # 让当前节点的next指向新节点
tail = node # 让tail也指向新节点
return head # 返回链表的head,可以通过head找到链表中的所有节点
def get_link_list(self, head):
""" 通过head获取链表的所有节点 """
while head: # 当head.next不为None,就循环输出
print(head.item, end=' ')
head = head.next
print()
def insert_node(self, head, key, element):
""" 插入,head是链表的头部,key表示插入的位置,element插入的元素 """
p = Node(element)
while head:
if head.item == key:
p.next = head.next
head.next = p
head = head.next # 用于循环,从head挨个往后找,直到遇到None
def remove_node(self, head, element):
""" 删除节点,head是链表的头部,element是要删除的元素 """
while head:
# 如果当前元素的下一个节点值等于element,那就让当前节点next指向下一个节点的下一个节点
if head.next.item == element:
head.next = head.next.next
break
head = head.next
else:
print('删除的元素[{}]不存在'.format(element))
lk = OperatorLinkList()
h = lk.create_link_list_head([1, 2, 3]) # 头插法创建单向链表
t = lk.create_link_list_tail([1, 2, 3]) # 尾插法创建单向链表
lk.get_link_list(t)
lk.insert_node(t, 1, 4)
lk.get_link_list(h)
lk.get_link_list(t)
lk.remove_node(t, 2)
lk.get_link_list(t)