王张开

Appearance

about ​

numpy是Python语言中做科学计算的基础库。

重在于数值计算，也是大部分Python科学计算库的基础。

它提供了各种高级数据编程工具，如矩阵运算、向量运算、快速筛选、IO操作、傅里叶变换、线性代数、随机数等。

注意，代码请在jupyter notebook环境下运行

numpy对象的创建 ​

通常有三种方式：

  • 使用np.array()创建
  • 使用plt创建
  • 使用np的routines函数创建

使用np.array()创建 ​

python
import numpy as np

# 创建一维数组
arr = np.array([1, 2, 3])
arr
"""
array([1, 2, 3])
"""
# 创建多维数组
arr = np.array([[1,2,3],[4,5,6]])
arr
"""
array([[1, 2, 3],
       [4, 5, 6]])
"""

我们通常将创建的arr对象称之为——ndarray对象，我们后续很多操作都是围绕ndarray对象展开的。

ndarray对象的属性 ​

必须掌握的几个属性：

  • ndim：维度
  • shape：形状（各维度的长度）
  • size：总长度
  • dtype：元素类型
python
import numpy as np

arr1 = np.array([1,2,3])
type(arr1), arr1.ndim, arr1.shape, arr1.size, arr1.dtype
"""
(numpy.ndarray, 1, (3,), 3, dtype('int32'))
"""

arr2 = np.array([[1,2,3],[2,3,4]])
type(arr2), arr2.ndim, arr2.shape, arr2.size, arr2.dtype
"""
(numpy.ndarray, 2, (2, 3), 6, dtype('int32'))
"""

ndarray对象和list的区别是啥 ​

  • 强制类型统一，ndarray数组中存储的数据元素类型必须是统一类型。
    • numpy默认ndarray的所有元素的类型是相同的。
    • 如果传进来的列表中包含不同的类型，则统一为同一类型，优先级：str>float>int
python
import numpy as np

list1 = [1,2,3, 4.12]
list1  # [1, 2, 3, 4.12]

arr2 = np.array([[1,2,3],[2,3,4]])
arr2
"""
array([[1, 2, 3],
       [2, 3, 4]])
"""

arr3 = np.array(list1)
arr3.dtype  # dtype('float64')


list2 = [1, 2, 3, 3.14, 'abc']
arr4 = np.array(list2)

# U 表示Unicode的简写形式
arr4.dtype  # dtype('<U32')


# 注意，内置函数type和dtype不太一样
type(arr2), arr2.dtype  # (numpy.ndarray, dtype('int32'))
# type 查看arr2对象本身的类型
# dtype查看arr2内部的元素类型，由于ndarray的元素类型是强制统一的，所以只返回一个类型

numpy的数据类型，了解 ​

名称描述
bool_布尔型数据类型（True 或者 False）
int_默认的整数类型（类似于 C 语言中的 long，int32 或 int64）
intc与 C 的 int 类型一样，一般是 int32 或 int 64
intp用于索引的整数类型（类似于 C 的 ssize_t，一般情况下仍然是 int32 或 int64）
int8字节（-128 to 127）
int16整数（-32768 to 32767）
int32整数（-2147483648 to 2147483647）
int64整数（-9223372036854775808 to 9223372036854775807）
uint8无符号整数（0 to 255）
uint16无符号整数（0 to 65535）
uint32无符号整数（0 to 4294967295）
uint64无符号整数（0 to 18446744073709551615）
float_float64 类型的简写
float16半精度浮点数，包括：1 个符号位，5 个指数位，10 个尾数位
float32单精度浮点数，包括：1 个符号位，8 个指数位，23 个尾数位
float64双精度浮点数，包括：1 个符号位，11 个指数位，52 个尾数位
complex_complex128 类型的简写，即 128 位复数
complex64复数，表示双 32 位浮点数（实数部分和虚数部分）
complex128复数，表示双 64 位浮点数（实数部分和虚数部分）

类型转换：astype ​

python
arr = np.array([0, 1, 2, 3])
arr    # array([0, 1, 2, 3])
arr.dtype  # dtype('int32'))

# 如果想要把数组中的元素转换为其它类型，就需要用到astype了
new_arr = arr.astype(np.float32)
arr		# array([0, 1, 2, 3])
arr.dtype  # dtype('int32')
new_arr	   # array([0., 1., 2., 3.], dtype=float32)
new_arr.dtype  # dtype('float32'))

jupyter notebook中的输出方式介绍 ​

在jupyter notebook中，有直接输出/print/display这几种输出方式。

python
import numpy as np

arr1 = np.array([1,2,3])
arr2 = np.array([[1,2,3],[2,3,4]])
# 直接输出
arr2
"""
array([[1, 2, 3],
       [2, 3, 4]])
"""

# print输出
print(arr2)
"""
[[1 2 3]
 [2 3 4]]
"""
print(arr1, arr2)
"""
[1 2 3] [[1 2 3]
 [2 3 4]]
"""
# display输出
display(arr2)
"""
array([[1, 2, 3],
       [2, 3, 4]])
"""
display(arr1, arr2)
"""
array([1, 2, 3])
array([[1, 2, 3],
       [2, 3, 4]])
"""

display相对于print输出更复杂且更直观一些。

所以，在jupyter notebook中，直接输出和display用的更多些。

routines函数创建ndarray对象 ​

routines函数指的是一系列快捷创建ndarray对象的相关函数。

  • np.ones，创建的数组默认值是1.0。
  • np.zeros，创建的数组默认值是0。
  • np.full，创建的数组可以通过fill_value来指定默认值。
  • np.eye，生成单位矩阵。
  • np.linspace和np.arange，用于生成等差数列的。
  • random系列，生成数组的值是随机的。

np.ones ​

np.ones(shape, dtype=None, order='C')

  • shape: 数组的形状，使用元组表示，几行几列
  • dtype：表示元素的类型
  • order：跟排序相关，我们一般不修改它，当成默认参数就行了，也不用传参
python
# 例如我们要创建如下数组
# 两行三列：(2,3)
[
    [1, 1, 1],
    [1, 1, 1]
]

# 三行一列：(3,1)
[
    [1],
    [1],
    [1],
]

# 一行三列：(1,3)
[
    [1,1,1]
]

# 只写个3呢？(3,) 它就是一维数组
[1,1,1]

# np.ones创建的数组，默认用1填充
np.ones(shape=(2,3))
"""
array([[1., 1., 1.],
       [1., 1., 1.]])
"""

# 如果是一维数组，下面几种写法是一样的
# np.ones(shape=(3,))
# np.ones(shape=(3))
np.ones(shape=3)    # array([1., 1., 1.])
np.ones(shape=(1,3))  # array([[1., 1., 1.]])

np.ones(shape=(3,1))
np.ones(shape=(3,2), dtype=np.int8)
"""
array([[1.],
       [1.],
       [1.]])
array([[1, 1],
       [1, 1],
       [1, 1]], dtype=int8)
"""

np.zeros ​

np.zeros(shape, dtype=float, order='C')

  • 用法和参数参考np.ones
python
# np.zeros创建的数组跟np.ones一样，只不过默认用0填充
np.zeros(shape=(3,1),dtype=np.uint8)
"""
array([[0],
       [0],
       [0]], dtype=uint8)
"""

np.full ​

np.full(shape, fill_value, dtype=None, order='C')

  • 用法和参数参考np.ones
python
# np.full就是创建的多维数组可以通过fill_value来指定默认值
np.full(shape=(3,3), fill_value=6)
"""
array([[6, 6, 6],
       [6, 6, 6],
       [6, 6, 6]])
"""

np.eye ​

np.eye(N, M=None, k=0, dtype=float) np.eye用于帮我们生成单位矩阵（identity matrix）

  • N：控制生成几阶的矩阵
  • M：控制列数
  • K：控制对角线的偏移量的
python
# 单位矩阵的简单特点就是从左上角到右下角的对角线（称为主对角线）上的元素均为1。 除此以外全都为0
# 如下
"""
1 0 0
0 1 0
0 0 1
"""

# np.eye就能帮我们快速生成如上的单位矩阵
np.eye(N=4)
"""
array([[1., 0., 0., 0.],
       [0., 1., 0., 0.],
       [0., 0., 1., 0.],
       [0., 0., 0., 1.]])
"""

# M：控制列数
np.eye(N=3, M=2)
"""
array([[1., 0.],
       [0., 1.],
       [0., 0.]])
"""

# K：控制对角线的偏移量的
np.eye(N=3, k=-1)
"""
array([[0., 0., 0.],
       [1., 0., 0.],
       [0., 1., 0.]])
"""

np.linspace和np.arange ​

np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

用于生成等差数列的。

  • start：起始位置
  • stop：结束位置
  • num：在区间内的生成元素的个数
  • endpoint：最后一个元素要不要
python
np.linspace(1, 10, 10)
# array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])

np.linspace(0, 100, 10, endpoint=False)
# array([ 0., 10., 20., 30., 40., 50., 60., 70., 80., 90.])

# endpoint的示例，比如我们生成一个圆的90度的四个点，应该是0,90,180,270
np.linspace(0, 360, 4)  # array([  0., 120., 240., 360.])

# 上面的360和0其实是重合的，所以我们需要endpoint来做，不要最后一个元素
np.linspace(0, 360, 4, endpoint=False)  # array([  0.,  90., 180., 270.])

np.arange([start, ]stop, [step, ]dtype=None)

np.linspace是在start和stop的区间内，生成元素的个数，而np.arange和它的区别是，np.arange是在区间内指定步长

python
np.arange(0, 100, step=10)
# array([ 0, 10, 20, 30, 40, 50, 60, 70, 80, 90])

random系列 ​

随机函数：np.random.randint ​

np.random.randint(low, high=None, size=None, dtype='l')

用于在指定大小范围内，生成矩阵，元素的值的大小在low和high之间随机取值。

  • low：最小值
  • high：最大值
  • size：维度，生成几行几列的数组
python
# 一维数组
np.random.randint(0,10, size=(10,))
np.random.randint(0, 10, size=(10))  # 这种写法也可以
np.random.randint(0,10, size=10) # 这种写法也可以
# array([9, 7, 2, 4, 3, 5, 6, 0, 7, 1])

# 多维数组
# 比如我们要生成一个3行5列的数组，元素的取值范围在0,100之间(包含0,100)
np.random.randint(low=0, high=100, size=(3,5))
"""
array([[82, 45, 19,  0, 43],
       [84, 78, 12, 66, 73],
       [96, 62, 78, 77, 49]])
"""

用的较多。

正态分布函数：np.random.randn和np.random.normal ​

正态分布是一种数据的分布形态，比如成年人的身高，从1米到2米这样的一个区间内，大多数人的身高是在1.75左右，所以数据越往中间越集中。

而np就能快捷的生成符合正态分布的数据。

  • np.random.randn(d0, d1, ..., dn) 标准正态分布
  • np.random.normal() 普通正态分布
python
# 例如生成一组身高的数组
np.random.normal(loc=175, scale=10, size=(10,))
# loc：期望值
# scale：标准方差
# size：生成的矩阵，几行几列
"""
array([184.60234182, 161.89002701, 186.56031925, 173.74428398,
       191.31591263, 178.92060179, 174.92974893, 182.84886133,
       182.39233675, 172.4764112 ])
"""

# 标准正态分布，就是标准方差固定为1，期望值固定为0的这样的一个矩阵
# 所以不需要传递loc和scale了，你想生成几维数组都直接传参即可
# 一维
np.random.randn(5)
# array([-0.47691045,  0.37666936,  0.17800342,  0.61167938,  1.1233994 ])

# 二维数组
np.random.randn(5, 2)
"""
array([[ 1.0993879 , -0.20840378],
       [-1.32859415,  0.32387861],
       [-1.33636594,  1.53103982],
       [-0.5848719 ,  2.58295395],
       [ 0.69017221, -0.64993494]])
"""

# 三维数组，更多维度依次类推
np.random.randn(5, 2, 2)
"""
array([[[ 0.46820421,  0.44779184],
        [-0.78187678,  2.84924511]],

       [[ 1.51163994, -0.65123959],
        [ 0.5746037 ,  1.4945258 ]],

       [[ 0.1754454 ,  0.82204765],
        [-1.42114934, -1.29865429]],

       [[ 0.7185443 ,  0.61174665],
        [-2.96566087,  0.15586061]],

       [[ 0.7197461 ,  0.80458074],
        [-0.47789594, -0.88786994]]])
"""

如果想展示分布结果，可以用matplotlib模块来做，比如我们展示下标准正态分布函数的数据分布结果：

python
import matplotlib.pyplot as plt

data = np.random.randn(10000)
plt.hist(data)
plt.savefig('./hist.png')
"""
(array([  12.,  108.,  515., 1549., 2732., 2738., 1617.,  603.,  113.,
          13.]),
 array([-3.74489925, -3.0012124 , -2.25752556, -1.51383871, -0.77015186,
        -0.02646502,  0.71722183,  1.46090868,  2.20459553,  2.94828237,
         3.69196922]),
 <BarContainer object of 10 artists>)
"""

1832669296178757632.png

0-1之间的随机数：np.random.random ​

np.random.random(size=None)

生成0到1之间的随机数，左闭右开，即有可能产生0，但不可能产生1。

python
np.random.random(size=(5,5))
"""
array([[0.27154428, 0.15353797, 0.9847046 , 0.6788529 , 0.56380613],
       [0.52390686, 0.51943157, 0.963915  , 0.79845016, 0.88624906],
       [0.01153064, 0.14995372, 0.54667128, 0.08854489, 0.45536732],
       [0.43948464, 0.50557079, 0.5827964 , 0.8424504 , 0.59003205],
       [0.98475124, 0.18346734, 0.37420967, 0.56733258, 0.57917978]])
"""

随机索引 ​

np.random.permutation(x) 生成随机索引。

python
# 注意，随机索引的最小值一定是0，因为索引就是从0开始的
np.random.permutation(10)
# array([9, 2, 8, 6, 3, 1, 7, 0, 5, 4])

随机种子 ​

用于锁定生成随机数，因为默认的，随机数每次运行都会改变，而随机种子就能控制或者说干扰随机数产生，有了随机种子，那么生成的随机数，无论怎么运行都是不变的。

python
# 没有随机种子的随机数，每次运行都会发生变化
np.random.randint(0,10, size=5)
# array([0, 1, 8, 8, 3])

# 有了随机种子，值就不变了
np.random.seed(1)  # 添加一个种子
np.random.randint(0,10, size=5)
# array([5, 8, 9, 5, 0])

小练习 ​

python
1. 创建一组形状为(3,4)，即3行4列的二维数组，取值范围为(-5，5)

2. 创建一组等差数列，步长为3， 数组长度为5

3. 构造一个3维取值范围为0-1的随机数组，数据类型为np.float64，形状为（3，3，3）

4. 已知π在numpy中是一个预制的常量，可以使用np.pi访问。计算出将一个圆等分成8份的弧度的代码
python
# 1. 创建一组形状为(3,4)，即3行4列的二维数组，取值范围为(-5，5)
np.random.randint(-5, 5, size=(3,4))
"""
array([[-5, -4,  2,  1],
       [ 4, -3, -1,  0],
       [-3, -1, -3, -1]])
"""

# 2. 创建一组等差数列，步长为3， 数组长度为5
# 用np.linspace和nparange都行
# np.linspace
np.linspace(0, 15, 5, endpoint=False)
# array([ 0.,  3.,  6.,  9., 12.])

# np.arange
np.arange(0, 15, step=3)
# array([ 0,  3,  6,  9, 12])


# 3. 构造一个3维的,取值范围为0-1的随机数组，数据类型为np.float64，形状为（3，3，3）
data = np.random.random(size=(3, 3, 3))
data
"""
array([[[0.39270739, 0.52198867, 0.80306595],
        [0.11634749, 0.21262935, 0.11550053],
        [0.13418651, 0.20120727, 0.67807024]],

       [[0.40220253, 0.13403904, 0.25294014],
        [0.43921594, 0.75765961, 0.59489539],
        [0.05422576, 0.84619319, 0.55857199]],

       [[0.70363642, 0.80842883, 0.58651706],
        [0.43087528, 0.74323492, 0.56027631],
        [0.02092122, 0.2179013 , 0.33378748]]])
"""
data.dtype  # dtype('float64')


# 4. 已知π在numpy中是一个预制的常量，可以使用np.pi访问。计算出将一个圆等分成8份的弧度的代码
# 思路：
# 首先π代表180°，半个圆
# 那么一个圆的完整弧度是2π，然后均分8分就完了
np.linspace(0, 2*np.pi, num=8, endpoint=False)
"""
array([0.        , 0.78539816, 1.57079633, 2.35619449, 3.14159265,
       3.92699082, 4.71238898, 5.49778714])
"""

ndarray对象的访问操作 ​

切片访问 ​

切片访问：

python
arr1 = np.random.randint(0, 100, size=10)
arr1  # array([71,  2, 46, 51, 99, 44, 51, 75, 23, 56])


# 索引也都是支持的
arr1[0], arr1[-1]

# 切片访问
arr1[0:3]  # array([71,  2, 46])
arr1[-4:]  # array([51, 75, 23, 56])
arr1[2:5]  #array([46, 51, 99])

带步长的：

python
arr1  # array([71,  2, 46, 51, 99, 44, 51, 75, 23, 56])
# arr1[start : end : step]
arr1[0:-1:2]  # array([71, 46, 99, 51, 23])
arr1[::-1]    # array([56, 23, 75, 51, 44, 99, 51, 46,  2, 71])
arr1[::-2]    # array([56, 75, 44, 51,  2])

重点来了，对于多维数组的访问

bash
ndarray的访问形式： 
    ndarray[dim1_index, dim2_index,...dimn_index]
dim_index支持的形式：
    int  [int, int]  切片  bool列表

示例：

python
arr2 = np.random.randint(0, 100, size=(5,5))
arr2
"""
array([[34, 24,  4, 32, 27],
       [86, 98, 57, 64, 69],
       [95, 66, 24, 60, 65],
       [93, 97, 75, 10, 11],
       [92, 58, 30, 23, 39]])
"""

dim_index的形式是：int

python
# 表示切出来数组的索引位置为1的行
arr2[1]  # array([86, 98, 57, 64, 69])

dim_index的形式是：[int, int]

python
# 表示取索引位置为1的行的第1列的值
arr2[1,1]  # 98

dim_index的形式是：切片

python
# 第一个冒号，表示全切整个数组，然后取出来第1,2列
arr2[:,[1,2]]
"""
array([[24,  4],
       [98, 57],
       [66, 24],
       [97, 75],
       [58, 30]])
"""
# 下面这种写法，0:2表示切出来数组的前两行，在对前两行进行切出来第1,2列
arr2[0:2, [1, 2]]
"""
array([[24,  4],
       [98, 57]])
"""
# 这种写法是反复的取行索引为1的值
arr2[[1, 1, 1 , 1,]]

dim_index的形式是：bool列表

python
arr3 = np.array([1, 2, 3, 4])
# 注意，布尔列表的长度必须和数组的维度一致，即数组有5列，布尔值列表要有5个元素
# 它会把索引位置为True的元素取出来
bool_index = [False, True, False, True, False]
arr3[bool_index]  # array([24, 11])

小练习来了

python
1. 构建一个长度为10的随机数组，进行逆序输出
2. 构造一个形状为(5,4)的二维数组，提取所有行的最后两列，使用3种方法
3. 构造一个形状为(5,4)的二维数组，提取前两行的最后两列，使用3种方法
python
# 1. 构建一个长度为10的随机数组，进行逆序输出
# 思路：逆序也就是翻转，可以用切片来完成
data1 = np.random.randint(0, 100, size=10)
display(data1, data1[::-1])
"""
array([89, 93, 84, 43,  4, 53, 68, 64,  9, 59])
array([59,  9, 64, 68, 53,  4, 43, 84, 93, 89])
"""
python
# 2. 构造一个形状为(5,4)的二维数组，提取所有行的最后两列，使用3种方法
data2 = np.random.randint(0, 100, size=(5,4))
display(data2)
"""
array([[13, 28, 86, 47],
       [36, 31, 51, 81],
       [59, 50, 32, 95],
       [13, 97, 48, 43],
       [94,  7, 11, 36]])
"""


# 方法1，切片取出来所有行，然后再取每行的最后两列
data2[:,[-2,-1]]
"""
array([[86, 47],
       [51, 81],
       [32, 95],
       [48, 43],
       [11, 36]])
"""

# 方法2，先切来所有行，在切片要后两列
data2[:, -2:]
"""
array([[86, 47],
       [51, 81],
       [32, 95],
       [48, 43],
       [11, 36]])
"""

# 方法3，采用bool列表，把后两列改为True即可
data2[:,[False, False, True, True]]
"""
array([[86, 47],
       [51, 81],
       [32, 95],
       [48, 43],
       [11, 36]])
"""

# 方法4，通常是列表和切片配合使用
data2[[0, 1, 2, 3, 4], -2:]    # 这个写法能行
"""
array([[86, 47],
       [51, 81],
       [32, 95],
       [48, 43],
       [11, 36]])
"""
# 但你不能这样写
# data2[[0, 1, 2, 3, 4], [-2, -1]]
python
# 3. 构造一个形状为(5,4)的二维数组，提取前两行的最后两列，使用3种方法
# 这个题的解题思路跟上一个题是一样的，上一题都是先切出来所有行，这里要直接切出来需要的前两行，在取后两列
data3 = np.random.randint(0, 100, size=(5,4))
data3
"""
array([[24, 46, 20, 31],
       [47, 46, 50, 98],
       [72,  1, 79, 10],
       [38, 34, 84, 22],
       [26, 47, 55,  7]])
"""

# 方法1
data3[:2,[-2, -1]]
# 方法2
data3[:2, -2:]
# 方法3
data3[:2, [False, False, True, True]]

# 上面三个结果一样
"""
array([[20, 31],
       [50, 98]])
"""

索引访问 ​

对于Python的列表来说：

python
# 对于一维数组，直接按照索引访问就行了
l1 = np.array([1, 2, 3, 4, 5])
l1  # array([1, 2, 3, 4, 5])
l1[0], arr[-1]  # (1, 5)

# 对于多维数组呢？比如二维数组
l2 = [[1,2,3],[2,3,4]]
l2  # [[1, 2, 3], [2, 3, 4]]
l2[1][0]   # 2

上面的按照索引方式，np中也是兼容的。

python
arr4 = np.random.randint(0, 10, size=10)
arr4  # array([7, 8, 1, 6, 3, 9, 6, 0, 7, 7])
arr4[0], arr4[-1]  # (7, 7)

arr5 = np.random.randint(0,10,size=(3,4))
arr5
"""
array([[2, 5, 5, 0],
       [0, 5, 9, 7],
       [3, 5, 4, 3]])
"""
arr5[2][1]  # 5

# 上面是读操作，写操作也是按照列表的操作一样，直接按索引赋值就行了
arr5[2][1] = 100
arr5
"""
array([[  2,   5,   5,   0],
       [  0,   5,   9,   7],
       [  3, 100,   4,   3]])
"""

【重点1】ndarray的高维数组访问，推荐使用[dim1_index, dim2_index...]

python
# 访问上面arr5中的第三维中的100
arr5[2, 1]  # 100


# 那么arr5[2,1]和arr5[2][1]有啥区别呢
arr5
"""
array([[  6,   2,   4,   1],
       [  7,   8,   5,   7],
       [  9, 100,   5,   5]])
"""

arr5[2][1] 
# 这种方式，也就是先通过arr5[2]拿到[  9, 100,   5,   5]，再从中拿到100，多了一步中间的操作
# 所以这种访问称为间接访问

# 而arr5[2,1]在np中对于高维数组的元素访问，是没有中间操作的，推荐这种写法
arr5[2,1]

列表的形式访问多个索引 ​

一维数组

python
arr1 = np.random.randint(0, 100, size=10)
arr1  # array([46, 96, 86, 81, 27, 45, 30, 90,  5,  3])

# 按照列表的操作访问多个索引
arr1[1], arr1[2]   # (96, 86)


# 那所谓以列表的形式访问多个索引，就是多个索引写成列表的形式
# 下面两种方式等价
index = [1, 2]
arr1[index]  # array([96, 86])
arr1[[1, 2]]  # array([96, 86])

那这种方式有啥好处呢？答案是可以反复按索引取值。

python
index1 = [1, 2, 1, 2, 1, 2]
arr1[index1]  # array([96, 86, 96, 86, 96, 86])


# 结合permutation来做列表的随机排序
# 拿到跟数组等长的索引列表
index2 = np.random.permutation(10)

# 相当于对原数组进行随机排序
arr1[index2]  # array([81, 90,  5,  3, 46, 96, 30, 45, 27, 86])

来个小练习，需求，随机的从arr1数组中取3个元素。

python
# 在原始数据中，随机取3个数
# 思路就是，先拿到随机索引
random_index = np.random.permutation(10)

# 从索引列表中切出来3个索引
random_index = np.random.permutation(10)[[0,1,2]]
random_index  # array([5, 3, 9])

# 对原列表进行按索引取值操作
arr1[random_index]  # array([45, 81,  3])

# 也可以这样
random_index2 = np.random.randint(0, 10, size=3)
random_index2  # array([6, 9, 2])
arr1[random_index2]  # array([30,  3, 86])

高维数组中使用

python
# 比如想要获取下面二维数组中的前两行，或者前两列
arr2 = np.random.randint(0, 100, size=(5,5))
arr2
"""
array([[73,  8, 18, 28, 22],
       [47, 15,  6, 63, 55],
       [89, 18,  2, 71, 30],
       [84, 91, 20, 82, 61],
       [44, 10,  5, 96, 92]])
"""

# 注意，传进去的是一个列表，列表中传递的是前两行的索引值
arr2[[0, 1]]
"""
array([[73,  8, 18, 28, 22],
       [47, 15,  6, 63, 55]])
"""

# 那如何获取前两列呢？我们可以借助列表的切片
arr2[:] 
"""
array([[73,  8, 18, 28, 22],
       [47, 15,  6, 63, 55],
       [89, 18,  2, 71, 30],
       [84, 91, 20, 82, 61],
       [44, 10,  5, 96, 92]])
"""

# 获取所有行的前两列
arr2[:,[0,1]]
"""
array([[73,  8],
       [47, 15],
       [89, 18],
       [84, 91],
       [44, 10]])
"""

# 获取前两行的前两列
arr2[0:2, [0, 1]]
"""
array([[73,  8],
       [47, 15]])
"""

ndarray的级联和切分 ​

级联就是将两个多维数组拼接成一个。

切分就是将一个数组切分为多个数组。

难点

这部分的难点就是你要对于轴axis的方向不迷糊，对于初学者来说，有点绕！迷糊了怎么办？反复琢磨琢磨吧。

级联 ​

级联也叫做拼接/相连，就是两个数组的拼接成一个数组。 关于轴axis参考相关帖子：

容易迷惑的点

就是轴的理解：

  • 一维数组：只能横向拼接，相当于Python中两个列表进行相加。
  • 二维数组，轴的方向参考下面那个图。
    • axis=0：
      • 横向(horizontal，水平方向)拼接，也就是沿着行进行拼接(垂直方向)。
      • 拼接后，行变，列不变。
      • 要求两个数组的行数不一致不影响，但列数必须一致，否则拼接失败。
    • axis=1：
      • 纵向(vertical，垂直方向)拼接，也就是沿着列进行拼接(水平方向)。
      • 拼接后，列变，行不变。
      • 要求两个数组的列数不一致不影响，但行数必须一致，否则拼接失败。

注意，级联操作只能同一维度的数组进行级联，比如2维和2维做级联，你不能2维和3维数组进行级联。

一维数组参考图：

python
# jupyter notebook中展示图片，把图片放到跟这个notebook文本同级目录下即可。
import matplotlib.pyplot as plt
%matplotlib inline
img = plt.imread('axis1.png')
plt.imshow(img)

1832669296329752576.png

二维数组参考图：

python
# jupyter notebook中展示图片，把图片放到跟这个notebook文本同级目录下即可。
import matplotlib.pyplot as plt
%matplotlib inline
img = plt.imread('axis2.png')
plt.imshow(img)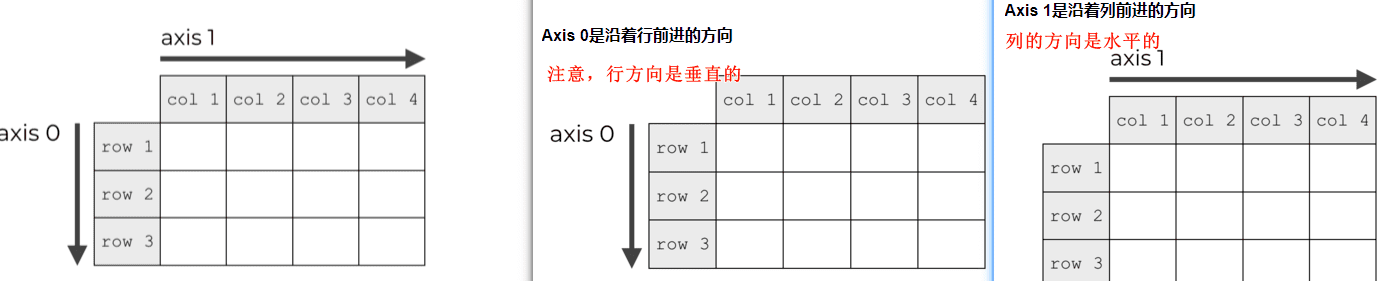

1832669296455581696.png

拼接常用的三个方法：

  • np.concatenate()，这个方法是通过axis值来决定方向的。
    • axis=0，默认值，横向拼接。拼接后，行变，列不变。要求列数必须一致。
    • axis=1，纵向拼接。拼接后，列变，行不变。要求行数必须一致。
  • 这俩方法相当于把np.concatenate()的功能进行拆分了。
    • np.vstack，等价于axis=0。拼接后，行变，列不变。要求列数必须一致。
    • np.hstack，等价于axis=1。拼接后，列变，行不变。要求行数必须一致。

一维数组级联 ​

一维数组的拼接，注意轴axis的值0，且方向是水平的。

python
a1 = np.random.randint(0, 10, size=3)
a2 = np.random.randint(0, 10, size=3)
display(a1, a2)
"""
array([5, 5, 8])
array([6, 7, 8])
"""

# 横向拼接
np.concatenate((a1, a2), axis=0)  # array([5, 5, 8, 6, 7, 8])

# 纵向拼接呢，一维数组只有一个轴，没法拼接
# np.concatenate((a1, a2), axis=1)

二维数组级联 ​

难度开始上来了。

默念口诀和注意观察上面的参考图片：

  • axis=0，默认值，横向拼接。拼接后，行变，列不变。要求列数必须一致。
  • axis=1，纵向拼接。拼接后，列变，行不变。要求行数必须一致。
python
a1 = np.random.randint(0, 10, size=(3,4))
a2 = np.random.randint(0,10,size=(4, 3))
a3 = np.random.randint(0,10,size=(4, 4))
display(a1, a2, a3)
"""
array([[1, 7, 3, 6],
       [8, 0, 0, 9],
       [3, 4, 5, 0]])
array([[1, 5, 8],
       [0, 1, 3],
       [9, 2, 0],
       [6, 1, 2]])
array([[1, 5, 8, 7],
       [9, 2, 5, 4],
       [1, 8, 4, 9],
       [2, 2, 8, 4]])
"""


# axis=0，a1和a3的列一致，可以横向拼接，结果行变，列不变。
np.concatenate((a1, a3), axis=0)
"""
array([[1, 7, 3, 6],
       [8, 0, 0, 9],
       [3, 4, 5, 0],
       [1, 5, 8, 7],
       [9, 2, 5, 4],
       [1, 8, 4, 9],
       [2, 2, 8, 4]])
"""

# axis=1，a2和a3的行一致，可以纵向拼接，结果列变，行不变。
np.concatenate((a2, a3), axis=1)
"""
array([[1, 5, 8, 1, 5, 8, 7],
       [0, 1, 3, 9, 2, 5, 4],
       [9, 2, 0, 1, 8, 4, 9],
       [6, 1, 2, 2, 2, 8, 4]])
"""

np.hstack与np.vstack

python
# np.vstack，等价于axis=0。拼接后，行变，列不变。要求列数必须一致。
# np.concatenate((a1, a3), axis=0)
np.vstack((a1, a3))
"""
array([[1, 7, 3, 6],
       [8, 0, 0, 9],
       [3, 4, 5, 0],
       [1, 5, 8, 7],
       [9, 2, 5, 4],
       [1, 8, 4, 9],
       [2, 2, 8, 4]])
"""

# np.hstack，等价于axis=1。拼接后，列变，行不变。要求行数必须一致。
# np.concatenate((a2, a3), axis=1)
np.hstack((a2, a3))
"""
array([[1, 5, 8, 1, 5, 8, 7],
       [0, 1, 3, 9, 2, 5, 4],
       [9, 2, 0, 1, 8, 4, 9],
       [6, 1, 2, 2, 2, 8, 4]])
"""

实操，关于级联的应用，使用numpy拼接图片

我要俩老婆

来一张美照：

python
# 图片来自：https://zh-yue.wikipedia.org/wiki/%E5%8A%89%E4%BA%A6%E8%8F%B2#/media/File:Liu_Yifei_Portrait1.jpg
import matplotlib.pyplot as plt
%matplotlib inline
img = plt.imread('lyf.jpg')
plt.imshow(img)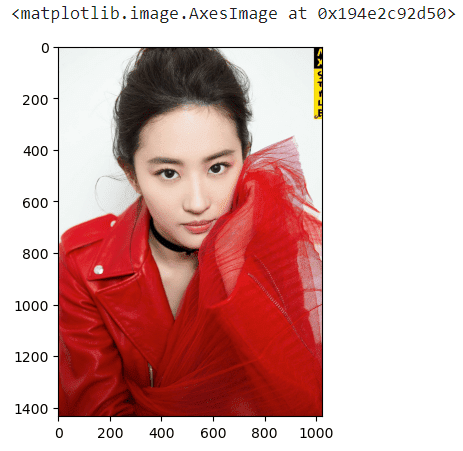

1832669296724017152.png

查看图片的各种属性：

python
# img是个三维数组
img  # 结果太长，省略.....

# 查看img的形状
img.shape  # (1434, 1024, 3)
# 在numpy中，图片通常是三维数组的形式表现
# 1434表示行数
# 1024表示列数
# 3表示RGB3通道

一个老婆变成俩老婆：

python
big_img = np.concatenate((img, img), axis=1)
plt.imshow(big_img)

# 保存图片
# plt.imsave('a.jpg', small_img)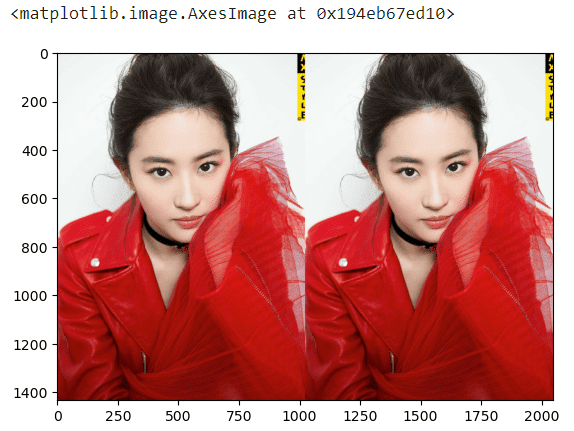

1832669296958898176.png

其它姿势：

python
# 左右翻转，第一和第三维不动，动第二维度
plt.imshow(big_img[:, ::-1, :])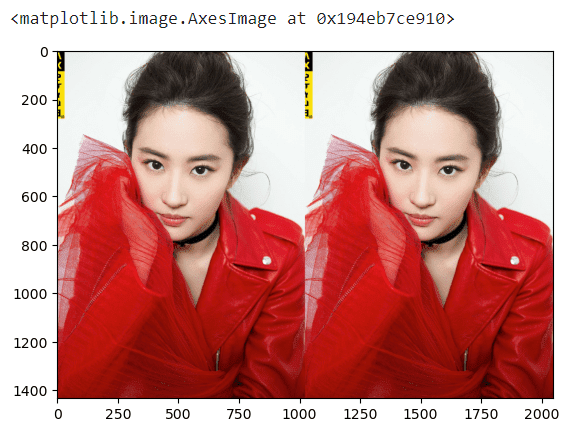

1832669297302831104.png

python
# 对图片进行上下翻转,也就是逆序下第一维数组，后两维不变
# plt.imshow(big_img[::-1, :, :])
plt.imshow(big_img[::-1,])  # 不变的后两维可以不写

1832669297596432384.png

python
# 裁剪图片，第三维不动
# 调整第一维，是上下裁剪
# 调整第二维，是左右裁剪
plt.imshow(big_img[0:900, 100:900, :])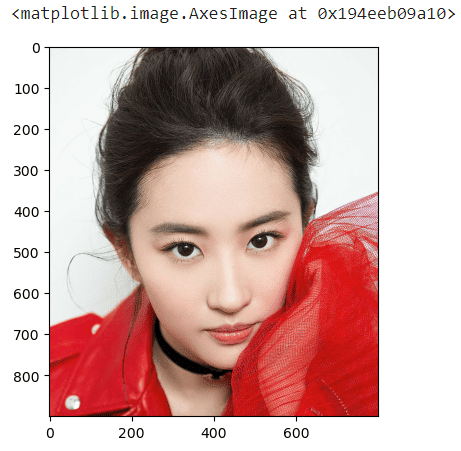

1832669297881645056.png

python
# 对图片进行压缩，比如每十个像素取一个像素
# 会得到一个压缩后的，模糊的图片
# small_img = big_img[::10, ::10]  # 第一二维每十个元素取一个元素，不动第三维
small_img = big_img[::10, ::10, :]  # 也可以这么写

# 展示图片
plt.imshow(small_img)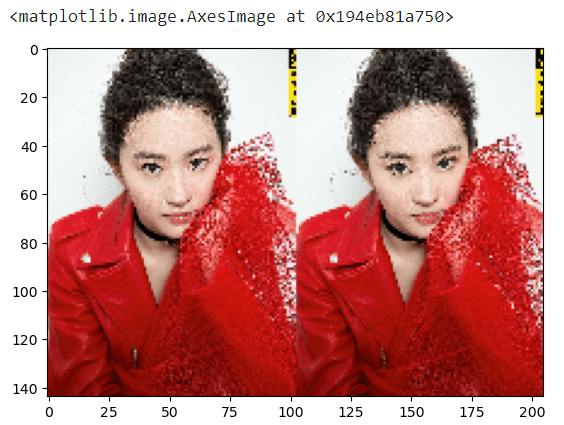

1832669298418515968.png

python
# 第1和第2维不动，动第3维度
# 结果就是颜色变了，因为只对第三维做了逆序，第三维的值是控制RGB颜色的值有变动，那么图片的颜色也跟着变动了
plt.imshow(big_img[:, :, ::-1])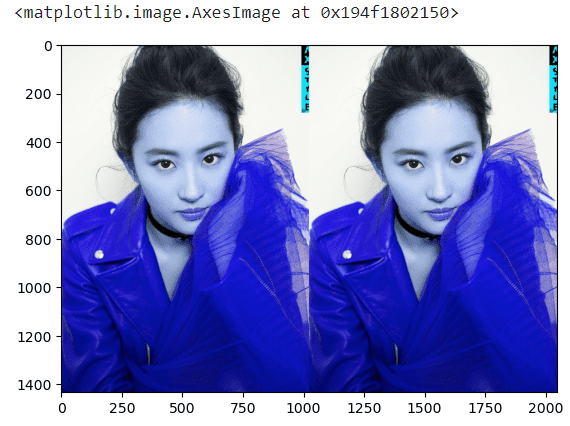

1832669299391594496.png

切分 ​

关于轴axis的理解，跟级联类似，三个函数完成切分工作：

  • np.split 通过axis的值控制方向，
    • axis=0，默认的，横向分割，是沿着行进行分割(垂直方向)。分割后，行变，列不变。
    • axis=1，纵向分割，就是沿着列进行分割(水平方向)。分割后，列边，行不变。
  • np.vsplit，等价于axis=0。分割后，行变列不变。
  • np.hsplit，等价于axis=1。分割后，列边行不变。
python
arr = np.random.randint(0, 100, size=(6,5))
arr
"""
array([[65, 46, 92, 55, 11],
       [64, 30, 99, 23, 17],
       [34, 19, 75, 10, 64],
       [46, 16, 34, 13, 72],
       [ 0, 18, 51, 67, 47],
       [ 7, 96, 36, 65, 33]])
"""

np.split方法，当indices_or_sections的值是整型时

python
# indices_or_sections int 会按照指定的轴向，将数组切分成N等分， 
# 要求切分的方向上的长度能被N整除
# 例如，如下示例中，axis=0决定切分方向是垂直方向，arr数组共有6行，所以
# 6能被2整除，切分后，行变列不变。
a1, a2 = np.split(arr, indices_or_sections=2, axis=0)
display(a1, a2)
"""
array([[65, 46, 92, 55, 11],
       [64, 30, 99, 23, 17],
       [34, 19, 75, 10, 64]])
array([[46, 16, 34, 13, 72],
       [ 0, 18, 51, 67, 47],
       [ 7, 96, 36, 65, 33]])
"""

# 但6不能被5整除，导致报错
# np.split(arr, indices_or_sections=5, axis=0)  # ValueError: array split does not result in an equal division

np.split方法，当indices_or_sections的值是列表时

python
# 即indices_or_sections=[m,n] 表示的是按照 0:m, m:n, n:最后 的切片逻辑对数组进行拆分 
# 注意是：左闭右开区间
arr = np.random.randint(0, 100, size=(7, 5))
arr
"""
array([[73, 60, 43,  8, 43],
       [33, 71, 49, 23, 87],
       [36, 50, 41,  1, 18],
       [90, 62, 93, 61, 45],
       [57, 38, 82, 26, 16],
       [41,  4, 36,  5, 22],
       [68, 56, 99, 14, 37]])
"""

# 写法1
np.split(arr, indices_or_sections=[3, 4], axis=0)
"""
[array([[73, 60, 43,  8, 43],
        [33, 71, 49, 23, 87],
        [36, 50, 41,  1, 18]]),
 array([[90, 62, 93, 61, 45]]),
 array([[57, 38, 82, 26, 16],
        [41,  4, 36,  5, 22],
        [68, 56, 99, 14, 37]])]
"""

# 写法2
np.split(arr, indices_or_sections=[2], axis=0)
# indices_or_sections=[2]的2表示先切前2行，后面的都算另一个数组的了
[array([[73, 60, 43,  8, 43],
        [33, 71, 49, 23, 87]]),
 array([[36, 50, 41,  1, 18],
        [90, 62, 93, 61, 45],
        [57, 38, 82, 26, 16],
        [41,  4, 36,  5, 22],
        [68, 56, 99, 14, 37]])]

注意，我上面演示的都是按行切割，也可以按照列切分，规则不变，

python
# 如果indices_or_sections的值是N,求切分的方向上的长度能被N整除，也就是列的长度要
# 能被N整除，当前arr的列长度是5，N是3，不能整除，所以不行
# np.split(arr, indices_or_sections=3, axis=1)

# 列表的写法是可以的
np.split(arr, indices_or_sections=[3], axis=1)
"""
[array([[73, 60, 43],
        [33, 71, 49],
        [36, 50, 41],
        [90, 62, 93],
        [57, 38, 82],
        [41,  4, 36],
        [68, 56, 99]]),
 array([[ 8, 43],
        [23, 87],
        [ 1, 18],
        [61, 45],
        [26, 16],
        [ 5, 22],
        [14, 37]])]
"""

# 这样也行
np.split(arr, indices_or_sections=[2, 3], axis=1)
"""
[array([[73, 60],
        [33, 71],
        [36, 50],
        [90, 62],
        [57, 38],
        [41,  4],
        [68, 56]]),
 array([[43],
        [49],
        [41],
        [93],
        [82],
        [36],
        [99]]),
 array([[ 8, 43],
        [23, 87],
        [ 1, 18],
        [61, 45],
        [26, 16],
        [ 5, 22],
        [14, 37]])]
"""

再来看np.vsplit和np.hsplit

python
# np.vsplit，等价于axis=0。分割后，行变列不变。
# 但不能切分，因为arr有5列，5不能被2整除
# np.split(arr, indices_or_sections=2, axis=0)
# np.vsplit(arr, indices_or_sections=2)


# np.hsplit，等价于axis=1。分割后，列边行不变。
# np.split(arr, indices_or_sections=[3], axis=1)
np.hsplit(arr, indices_or_sections=[3])
"""
[array([[73, 60, 43],
        [33, 71, 49],
        [36, 50, 41],
        [90, 62, 93],
        [57, 38, 82],
        [41,  4, 36],
        [68, 56, 99]]),
 array([[ 8, 43],
        [23, 87],
        [ 1, 18],
        [61, 45],
        [26, 16],
        [ 5, 22],
        [14, 37]])]
"""

小练习来了 ​

python
1. 生成两个形状分别为（4，4）和（8，4）的二维整型数组，尝试进行横向和纵向级联
2. 使用两种方法将上题级联的结果保存并拆分成3等份
3. 生成一个长度为5的一维整型数组，将类型修改为float32
python
# 1. 生成两个形状分别为（4，4）和（8，4）的二维整型数组，尝试进行横向和纵向级联
# 口诀：横向连接看列数，列数一致就能连；纵向连接看行数，行数一致就能连
# a1和a2能横着连；不能纵着连
a1 = np.random.randint(0, 10, size=(4,4))
a2 = np.random.randint(0, 10, size=(8,4))
display(a1, a2)
"""
array([[9, 3, 4, 1],
       [8, 3, 1, 0],
       [7, 7, 7, 2],
       [1, 3, 1, 5]])
array([[2, 1, 4, 6],
       [7, 4, 3, 4],
       [9, 9, 7, 3],
       [8, 6, 2, 4],
       [7, 2, 8, 8],
       [6, 6, 3, 6],
       [6, 0, 2, 8],
       [1, 9, 4, 7]])
"""
# 横着连，列数一样，能连
np.concatenate((a1, a2), axis=0)
"""
array([[9, 3, 4, 1],
       [8, 3, 1, 0],
       [7, 7, 7, 2],
       [1, 3, 1, 5],
       [2, 1, 4, 6],
       [7, 4, 3, 4],
       [9, 9, 7, 3],
       [8, 6, 2, 4],
       [7, 2, 8, 8],
       [6, 6, 3, 6],
       [6, 0, 2, 8],
       [1, 9, 4, 7]])
"""


# 纵着连,行数不一样，不能连
# np.concatenate((a1, a2), axis=1)
python
# 2. 使用两种方法将上题级联的结果保存并拆分成3等份
# 先保存拼接结果
a1 = np.random.randint(0, 10, size=(4,4))
a2 = np.random.randint(0, 10, size=(8,4))
arr = np.concatenate((a1, a2), axis=0)
arr
"""
array([[9, 3, 4, 1],
       [8, 3, 1, 0],
       [7, 7, 7, 2],
       [1, 3, 1, 5],
       [2, 1, 4, 6],
       [7, 4, 3, 4],
       [9, 9, 7, 3],
       [8, 6, 2, 4],
       [7, 2, 8, 8],
       [6, 6, 3, 6],
       [6, 0, 2, 8],
       [1, 9, 4, 7]])
"""

# 对拼接结果进行拆分
np.split(arr, indices_or_sections=3, axis=0)
"""
[array([[9, 3, 4, 1],
        [8, 3, 1, 0],
        [7, 7, 7, 2],
        [1, 3, 1, 5]]),
 array([[2, 1, 4, 6],
        [7, 4, 3, 4],
        [9, 9, 7, 3],
        [8, 6, 2, 4]]),
 array([[7, 2, 8, 8],
        [6, 6, 3, 6],
        [6, 0, 2, 8],
        [1, 9, 4, 7]])]
"""
python
# 3. 生成一个长度为5的一维整型数组，将类型修改为float32
data = np.random.randint(0, 10, size=5)
data	# array([6, 7, 4, 9, 6])
data.dtype  # dtype('int32')

# astype()
# ndarray 实例方法， 这个方法是将ndarray对象内的每一个元素进行指定的类型转换
data.astype(np.float32)  # array([6., 7., 4., 9., 6.], dtype=float32)

变形函数：reshape ​

变形指得是改变数组的形状，比如一维数组改变为二维数组。

python
# 将二维数组改变为一维
arr = np.random.randint(0, 100, size=(3, 4))

# 原始二维数组的总元素个数是3 * 4 = 12
# 那么改变成一维之后，也要有12个元素位置，多了少了都不行
new_arr = arr.reshape(12)
display(arr, new_arr)
"""
array([[61, 45,  0, 37],
       [25, 60,  3, 94],
       [21, 94, 41, 39]])
array([61, 45,  0, 37, 25, 60,  3, 94, 21, 94, 41, 39])
"""

# 一维变多维也是相同逻辑
# new_arr这个一维数组此时有12个元素，那么创建的二维数组或者多维数组的
# 元素总个数也要和new_arr一致
# 一维变二维
# new_arr.reshape((1, 12))
# new_arr.reshape((2, 6))
# new_arr.reshape((3, 4))

# 一维变多维
# new_arr.reshape((2, 2, 3))

# 注意，shape参数不能显式使用，用了报错
# 直接传元组就行了
# new_arr.reshape(shape=(2, 2, 3))  # TypeError: 'shape' is an invalid keyword argument for this function

ndarray的运算 ​

基本运算规则 ​

两个矩阵的运算，本质上就是对应位置的数据的运算。

来个示例，来两个一维数组。

python
a1 = np.random.random(10)
a2 = np.random.randint(0, 10, size=10)
a1
a2
"""
array([0.98105538, 0.84210888, 0.14050005, 0.18817351, 0.09281394,
        0.13027877, 0.53499164, 0.22320665, 0.66295515, 0.12997677]),
array([9, 0, 9, 6, 1, 5, 4, 4, 7, 6])
"""

# 如果两个数组的长度一致，那么对应索引位置的元素就可以相加
a1 + a2
"""
array([9.98105538, 0.84210888, 9.14050005, 6.18817351, 1.09281394,
       5.13027877, 4.53499164, 4.22320665, 7.66295515, 6.12997677])
"""

上面那种套路同样适用于多维数组：

python
a3 = np.random.randint(1, 10, size=(3, 3))
a4 = np.random.randint(1, 10, size=(3, 3))
a3, a4
"""
(array([[6, 1, 1],
        [8, 6, 7],
        [7, 2, 9]]),
 array([[4, 8, 1],
        [7, 3, 9],
        [2, 3, 2]]))
"""

a3 + a4
"""
array([[10,  9,  2],
       [15,  9, 16],
       [ 9,  5, 11]])
"""

注意，运算不只是包含上面示例中的算术运算，还包括Python中的各种运算，都属于该运算的范畴内。

python
# 随便举个例子，比较运算
a3 > a4
"""
array([[ True, False, False],
       [ True,  True, False],
       [ True, False,  True]])
"""

再来个例子，一个二维数组和一个普通的数字可以进行运算:

python
a3 > 4
"""
array([[ True, False, False],
       [ True,  True,  True],
       [ True, False,  True]])
"""

是不很牛逼，它是怎么做到让4和每个元素都进行比较的呢？这就牵扯到numpy中的广播机制了。

广播机制Broadcast ​

广播仍然遵循运算机制，即：两个矩阵运算，就是对应位置的数据的运算。

ndarray广播机制的两条规则

符合其中一条就行：

  1. 如果两个数组的后缘维度（trailing dimension，即从末尾开始算起的维度）的轴长度相符。
  2. 或者其中的一方的长度为1。

则认为它们是广播兼容的。 广播会在缺失和（或）长度为1的维度上进行。

如何理解，第一个条件呢？什么是后缘维度呢？

python
# 比如下面两个数组中，后缘维度指的是从最后开始往左看，2,3都是相同的，所以我们可以说这俩数组
# 后缘维度相同，且最后一位一样，我们说轴长度相符
(3, 2)
(4, 3, 2)

# 或者下面的也行
(3, 2)
(2, )


# 下面这种就不行,2和1不相符
(3, 2)
(4, 3, 1)

例1：a = np.ones((2, 3)) b = np.arange(3) 求a + b

python
# 首先这俩数组后缘维度相同，符合广播条件，可以进行运算
a = np.ones((2,3))
b = np.arange(3)
display(a, b)
"""
array([[1., 1., 1.],
       [1., 1., 1.]])
array([0, 1, 2])
"""

# 运算结果
a + b
"""
array([[1., 2., 3.],
       [1., 2., 3.]])
"""

# 原理就是numpy内部先将两个不同的维度的数组搞成同等维度就行了
# 那就是把一维数组变形为二维数组，然后再进行运算
c = [
    [0, 1, 2],
    [0, 1, 2],
]
a + c
"""
array([[1., 2., 3.],
       [1., 2., 3.]])
"""

例2: a = np.ones((4,3,2)), b = np.random.randint(0,10,size=(3,2)), 求a+b

python
# 这俩数组后缘维度相同，符合广播条件，可以进行运算
# 内部运算逻辑也是转为相同维度的数组后再计算
a = np.ones((4, 3, 2))
b = np.random.randint(0, 10, size=(3, 2))
display(a, b)
"""
array([[[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]]])
array([[1, 3],
       [7, 2],
       [2, 7]])
"""

# 运算结果
a + b
"""
array([[[2., 4.],
        [8., 3.],
        [3., 8.]],

       [[2., 4.],
        [8., 3.],
        [3., 8.]],

       [[2., 4.],
        [8., 3.],
        [3., 8.]],

       [[2., 4.],
        [8., 3.],
        [3., 8.]]])
"""

那又如何理解第二个条件，"其中的一方的长度为1"这个条件呢

也就是说，只要有一个数组的长度是为1的，那么就可以运算。

举个例子：

例3：a = np.arange(3).reshape((3, 1)), b = np.arange(3), 求a+b

python
# a是2维数组，且它的长度为1，另一个数组为一维数组
# 那么它内部就能变形成同一维度的数组，然后再计算
a = np.arange(3).reshape((3,1))  # 注意，a是二维数组
b = np.arange(3)
# 三维数组想要也能参与运算，则需要满足长度和维度和一维数组的长度相等
# 毕竟内部也要转成一致的维度后才能可以
c = np.arange(27).reshape((3, 3, 3))
display(a, b, c)
"""
array([[0],
       [1],
       [2]])
array([0, 1, 2])
array([[[ 0,  1,  2],
        [ 3,  4,  5],
        [ 6,  7,  8]],

       [[ 9, 10, 11],
        [12, 13, 14],
        [15, 16, 17]],

       [[18, 19, 20],
        [21, 22, 23],
        [24, 25, 26]]])
"""

# 符合条件的二维 + 一维是可以运算的
a + b
"""
array([[0, 1, 2],
       [1, 2, 3],
       [2, 3, 4]])
"""

# 符合条件的三维数组也可以和一维数组进行运算
a + c
"""
array([[[ 0,  1,  2],
        [ 4,  5,  6],
        [ 8,  9, 10]],

       [[ 9, 10, 11],
        [13, 14, 15],
        [17, 18, 19]],

       [[18, 19, 20],
        [22, 23, 24],
        [26, 27, 28]]])
"""

# 这个就不用说了，它符合后缘维度相同
b + c
"""
array([[[ 0,  2,  4],
        [ 3,  5,  7],
        [ 6,  8, 10]],

       [[ 9, 11, 13],
        [12, 14, 16],
        [15, 17, 19]],

       [[18, 20, 22],
        [21, 23, 25],
        [24, 26, 28]]])
"""

再来看另一个概念，ndarray可以跟任意的整数进行广播运算

python
arr = np.random.randint(0, 5, size=(3, 3))
arr
"""
array([[2, 2, 0],
       [4, 1, 2],
       [2, 0, 4]])
"""

a + 1
"""
array([[1],
       [2],
       [3]])
"""

小练习来了 ​

bash
1. a = np.ones((4, 1)), b = np.arange(4), 求a+b
2. 假设我们有100个员工考勤需要处理，由于上个月统一调休，所以需要将所有人的总考勤天数-1，如何操作？
3. 假设员工上班时间表通过np.random.randint(7,10,100)获取,如何快速找到上班时间不足8小时的员工？
python
# 1. a = np.ones((4, 1)), b = np.arange(4), 求a+b
a = np.ones((4, 1))
b = np.arange(4)
a, b
"""
(array([[1.],
        [1.],
        [1.],
        [1.]]),
 array([0, 1, 2, 3]))
"""
a + b
"""
array([[1., 2., 3., 4.],
       [1., 2., 3., 4.],
       [1., 2., 3., 4.],
       [1., 2., 3., 4.]])
"""
python
# 2. 假设我们有100个员工考勤需要处理，由于上个月统一调休，
# 所以需要将所有人的总考勤天数-1，如何操作？

# 生成100个员工的考勤
data = np.random.randint(20, 23, size=100)
data
"""
array([21, 20, 21, 22, 22, 20, 21, 21, 21, 22, 20, 21, 20, 21, 21, 21, 22,
       21, 21, 21, 21, 21, 21, 22, 21, 22, 20, 21, 20, 21, 22, 22, 20, 21,
       21, 21, 21, 20, 20, 21, 20, 22, 22, 21, 22, 22, 22, 22, 22, 22, 20,
       22, 21, 22, 20, 22, 22, 20, 22, 22, 22, 20, 21, 21, 20, 22, 21, 21,
       22, 22, 22, 21, 21, 21, 22, 22, 22, 21, 21, 20, 22, 21, 20, 22, 20,
       20, 22, 20, 21, 21, 21, 20, 21, 22, 21, 22, 21, 20, 21, 20])
"""

# 总考勤减一操作，其实就是让数组内的每个元素都自减一
new_data = data - 1
new_data
"""
array([20, 19, 20, 21, 21, 19, 20, 20, 20, 21, 19, 20, 19, 20, 20, 20, 21,
       20, 20, 20, 20, 20, 20, 21, 20, 21, 19, 20, 19, 20, 21, 21, 19, 20,
       20, 20, 20, 19, 19, 20, 19, 21, 21, 20, 21, 21, 21, 21, 21, 21, 19,
       21, 20, 21, 19, 21, 21, 19, 21, 21, 21, 19, 20, 20, 19, 21, 20, 20,
       21, 21, 21, 20, 20, 20, 21, 21, 21, 20, 20, 19, 21, 20, 19, 21, 19,
       19, 21, 19, 20, 20, 20, 19, 20, 21, 20, 21, 20, 19, 20, 19])
"""
python
# 3. 假设员工上班时间表通过np.random.randint(7,10,100)获取,
# 如何快速找到上班时间不足8小时的员工？

# 100个员工的上班时间
data = np.random.randint(7, 10, size=100) 
data
"""
array([9, 9, 7, 7, 9, 9, 7, 9, 8, 9, 7, 7, 9, 9, 8, 9, 8, 8, 8, 8, 7, 8,
       7, 7, 9, 9, 7, 9, 8, 8, 9, 7, 8, 7, 8, 8, 8, 7, 8, 7, 8, 9, 7, 7,
       9, 7, 8, 7, 9, 9, 7, 8, 8, 9, 8, 8, 8, 9, 7, 8, 7, 7, 9, 9, 9, 8,
       9, 7, 9, 8, 7, 7, 7, 7, 9, 7, 8, 7, 7, 7, 9, 7, 8, 9, 7, 9, 7, 9,
       9, 8, 8, 8, 9, 7, 9, 7, 9, 9, 8, 9])
"""

# 让每个元素跟8作比较
new_data = data < 8
new_data
"""
array([False, False,  True,  True, False, False,  True, False, False,
       False,  True,  True, False, False, False, False, False, False,
       False, False,  True, False,  True,  True, False, False,  True,
       False, False, False, False,  True, False,  True, False, False,
       False,  True, False,  True, False, False,  True,  True, False,
        True, False,  True, False, False,  True, False, False, False,
       False, False, False, False,  True, False,  True,  True, False,
       False, False, False, False,  True, False, False,  True,  True,
        True,  True, False,  True, False,  True,  True,  True, False,
        True, False, False,  True, False,  True, False, False, False,
       False, False, False,  True, False,  True, False, False, False,
       False])
"""

数组的append/insert/delete操作 ​

append添加元素 ​

numpy.append 函数在数组的末尾添加值。 追加操作会分配整个数组，并把原来的数组复制到新数组中。

  • 添加的维度要保证所有数组的长度是相同的。
  • 如果没有指定轴，数组会被扁平处理，也就是变成一维的情况。
python
arr1 = np.array([1,2,3,4])
arr1  # array([1, 2, 3, 4])

# 不能arr1.append，会报错
# arr.append(5)  # AttributeError: 'numpy.ndarray' object has no attribute 'append'

# 而是要用np.append
np.append(arr1, 8)  # array([1, 2, 3, 4, 8])
python
arr2 = np.random.randint(0, 10, size=(4,3))
arr2
"""
array([[9, 7, 6],
       [7, 2, 7],
       [8, 5, 6],
       [3, 3, 5]])
"""

# axis=0，横向添加，行变列不变。
# 添加数组的维度要和原数组的维度相同，即原数组是二维数组，append的数组也要是二维的
# 否则会报错
# np.append(arr2, [1,2,3], axis=0)  # 报错

# append的也是二维的，且长度跟原数组一致，都是3列
np.append(arr2, [[1,2,3]], axis=0)
"""
array([[9, 7, 6],
       [7, 2, 7],
       [8, 5, 6],
       [3, 3, 5],
       [1, 2, 3]])
"""

# axis=1，纵向添加，列变行不变。
# 因为arr2是4行3列的二维数组，想要纵向插入，则要保证行不变，有几列无所谓
arr2 = np.random.randint(0, 10, size=(4,3))
arr3 = np.ones(shape=(4,2))
display(arr2, arr3)
"""
array([[9, 5, 4],
       [2, 9, 9],
       [6, 9, 4],
       [0, 6, 6]])
array([[1., 1.],
       [1., 1.],
       [1., 1.],
       [1., 1.]])
"""

arr4 = np.append(arr2, arr3, axis=1)
# append不是原地操作，而是会创建一个新的数组
display(arr2, arr4)
"""
array([[9, 5, 4],
       [2, 9, 9],
       [6, 9, 4],
       [0, 6, 6]])
array([[9., 5., 4., 1., 1.],
       [2., 9., 9., 1., 1.],
       [6., 9., 4., 1., 1.],
       [0., 6., 6., 1., 1.]])
"""

# 注意，如果添加时，不指定轴，则数组会被展开
arr5 = np.append(arr2, arr3)
arr5
"""
array([9., 5., 4., 2., 9., 9., 6., 9., 4., 0., 6., 6., 1., 1., 1., 1., 1.,
       1., 1., 1.])
"""

insert插入元素 ​

numpy.insert 函数在给定索引之前，沿给定轴在输入数组中插入值

多维数组的情况下，如果未提供轴，则输入数组会被展开。

python
# 一维数组的插入
arr = np.random.randint(0, 10, size=5)
arr  # array([7, 0, 4, 1, 2])

# 可以在指定索引位置之前插入数值和列表
np.insert(arr, 1, 1)  # array([7, 1, 0, 4, 1, 2])
np.insert(arr, 1, [4, 4])  # array([7, 4, 4, 0, 4, 1, 2])
python
# 二维数组的插入
arr = np.random.randint(0, 10, size=(4, 3))
arr
"""
array([[8, 1, 5],
       [5, 3, 8],
       [8, 7, 3],
       [5, 9, 5]])
"""

# axis=0，横向插入，垂直方向发生变化，行变列不变。
# 多维数组的情况下，如果未提供轴，则输入数组会被展开
display(arr, np.insert(arr, 1, [1, 1, 1]))
"""
array([[8, 1, 5],
       [5, 3, 8],
       [8, 7, 3],
       [5, 9, 5]])
array([8, 1, 1, 1, 1, 5, 5, 3, 8, 8, 7, 3, 5, 9, 5])
"""

# 指定轴就可以了
display(arr, np.insert(arr, 1, [1, 1, 1], axis=0))
"""
array([[8, 1, 5],
       [5, 3, 8],
       [8, 7, 3],
       [5, 9, 5]])
array([[8, 1, 5],
       [1, 1, 1],
       [5, 3, 8],
       [8, 7, 3],
       [5, 9, 5]])
"""

# axis=1，纵向插入，水平方向发生变化，列变行不变。
display(arr, np.insert(arr, 1, [1, 1, 1, 1], axis=1))
"""
array([[8, 1, 5],
       [5, 3, 8],
       [8, 7, 3],
       [5, 9, 5]])
array([[8, 1, 1, 5],
       [5, 1, 3, 8],
       [8, 1, 7, 3],
       [5, 1, 9, 5]])
"""

delete删除元素 ​

numpy.delete函数返回从输入数组中删除指定子数组的新数组。

如果未提供轴参数，则输入数组将展开。

python
# 一维数组的删除，删除的是指定索引位置的元素
arr = np.random.randint(0, 10, size=5)
display(arr, np.delete(arr, 1))  
"""
array([2, 7, 1, 8, 2])
array([2, 1, 8, 2])
"""
python
# 二维数组的删除
arr = np.random.randint(0, 10, size=(4, 3))
arr
"""
array([[1, 0, 8],
       [0, 9, 6],
       [6, 1, 9],
       [0, 3, 6]])
"""


# 如果未提供axis轴参数，则输入数组将展开。
display(arr, np.delete(arr, 1))  
# 把第一行索引为1的元素删除了，然后按顺序把数组展开为1维的
"""
array([[1, 0, 8],
       [0, 9, 6],
       [6, 1, 9],
       [0, 3, 6]])
array([1, 8, 0, 9, 6, 6, 1, 9, 0, 3, 6])
"""


# axis=0，横向删除，行变列不变。
display(arr, np.delete(arr, 1, axis=0))
"""
array([[1, 0, 8],
       [0, 9, 6],
       [6, 1, 9],
       [0, 3, 6]])
array([[1, 0, 8],
       [6, 1, 9],
       [0, 3, 6]])
"""

# axis=1，纵向删除，列变行不变。
display(arr, np.delete(arr, 1, axis=1))
"""
array([[1, 0, 8],
       [0, 9, 6],
       [6, 1, 9],
       [0, 3, 6]])
array([[1, 8],
       [0, 6],
       [6, 9],
       [0, 6]])
"""

其他操作 ​

数组迭代器 ​

arr.flat返回一维或者多维数组的迭代器：

python
import numpy as np

arr1 = np.random.randint(0, 10, size=10)
arr2 = np.random.randint(0, 10, size=(3, 3))
arr2 = np.random.randint(0, 10, size=(3, 3, 3))
display(arr1.flat, arr2.flat, arr3.flat)
"""
<numpy.flatiter at 0x1cc3880c950>
<numpy.flatiter at 0x1cc385d45a0>
<numpy.flatiter at 0x1cc385d3080>
"""
for i in arr1.flat:
    print(i, end=" ")
for i in arr2.flat:
    print(i, end=" ")
for i in arr3.flat:
    print(i, end=" ")
"""
1 3 6 1 1 8 7 8 0 8 
1 6 1 1 0 4 1 7 7 0 3 3 0 0 9 5 9 7 2 8 8 3 6 7 9 8 7 
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 
"""

数组扁平处理 ​

所谓扁平处理，就是将多维数组展开为一维数组，常用的两个函数：

  • arr.flatten()，返回一份展开的数组拷贝副本，对拷贝副本所做的修改不会影响原始数组，相当于Python的深拷贝。
  • arr.ravel()，展平的数组元素，返回一个展开的数组引用，修改会影响原始数组，相当于Python的浅拷贝。
python
import numpy as np

arr = np.random.randint(1, 10, size=(3, 4))
display(arr, arr.flatten(), arr.ravel())
"""
array([[2, 7, 8, 5],
       [1, 2, 9, 5],
       [4, 8, 5, 6]])
array([2, 7, 8, 5, 1, 2, 9, 5, 4, 8, 5, 6])
array([2, 7, 8, 5, 1, 2, 9, 5, 4, 8, 5, 6])
"""

数组翻转 ​

这里的数组翻转指的是数据维度的调换。

python
import numpy as np

arr2 = np.random.randint(0, 10, size=(4, 3))
display(arr2, arr2.shape)
"""
array([[7, 8, 7],
       [0, 1, 9],
       [6, 1, 4],
       [4, 6, 7]])
(4, 3)
"""
# 对数组的维度进行翻转，效果就是每行的列组成新的行
arr2.transpose([1, 0])
"""
array([[7, 0, 6, 4],
       [8, 1, 1, 6],
       [7, 9, 4, 7]])
"""

常用函数一览 ​

numpy封装了很多的数学上的函数。我们来大致看看。

聚合函数 ​

常用的聚合函数：

Function NameNaN-safe VersionDescription
np.sumnp.nansum求和
np.prodnp.nanprod求积
np.meannp.nanmean求平均
np.stdnp.nanstd计算标准偏差
np.varnp.nanvar计算方差
np.minnp.nanmin查找最小值
np.maxnp.nanmax查找最大值
np.mediannp.nanmedian计算数组的中位数
np.percentilenp.nanpercentile求百分位数
np.anyN/A数组中只要有一个为True，则返回True
np.allN/A数组中全为True，则返回True

求和、空值的处理

python
# 一维数组的求和
data = np.random.randint(0, 10, size=5)
display(data, data.sum())
"""
array([5, 3, 2, 5, 4])
19
"""

# 高维数组的求和
# sum默认求的是整个高维数组的元素之和
data = np.random.randint(0, 10, size=(3,2))
display(data, data.sum())
"""
array([[2, 7],
       [7, 6],
       [8, 9]])
39
"""

# 求每一行的和，垂直方向所有行的同一列累加
data.sum(axis=0)  # array([17, 22])


# 求每一列的和， 水平方向，每行累加
data.sum(axis=1)  # array([ 9, 13, 17])
python
"""
如果数组中存在空值的话，我们该如何处理呢？ 这里要先补充下关于numpy关于空值的处理。 
Python中空值用None表示，类型是NoneType。
而numpy中空值用np.nan表示，类型是float，为什么是float类型，为了运算时保证类型统一，所以这点和Python不太一样。
np.nan的另一个特点是它和任何数进行算术运算都得空。
"""
# 进行算术运算都得空
a = np.nan - 1  
b = np.nan + 1
c = np.nan * 1
display(a, b, c)
"""
nan
nan
nan
"""
python
"""
了解了空值之后，我们来研究下如果数组中出现空值，该如何处理
"""
# 因为空值是float类型，所以，这里创建数组时就生命好类型为float，好方便后面赋值
data = np.arange(0, 10, 2, dtype=np.float32)
data  # array([0., 2., 4., 6., 8.], dtype=float32)

# 赋空值
data[1] = np.nan
data  # array([ 0., nan,  4.,  6.,  8.], dtype=float32)

# 带有空值的求和，结果是nan
data.sum()  # nan

# numpy为了解决nan的问题，封装了一系列处理nan类型的函数
# 比如求和不带nan的，用sum就行了
# 带nan的，用nansum
np.nansum(data)  # 18.0

最大最小、求平均

python
arr = np.arange(0, 10, 2)
arr  # array([0, 2, 4, 6, 8])

arr.max(), arr.min(), arr.mean()
# (8, 0, 4.0)

其他的不在演示了，百度一下都有的。

any和all

这俩函数的作用是：

  • np.any()，一个数组中，所有元素至少存在一个True, any函数就返回True。
  • np.all()，一个数组中，所有元素全都是True, all函数就返回True。
python
# 来个示例
a1 = np.array([False, False, True, True])
a2 = np.array([True, True, True, True])
# 也可以这么构造
# a3 = np.random.randint(0, 2, size=10).astype(np.bool)

display(a1.any(), a2.all())
"""
True
True
"""


# 示例2
# 问题：score是20个学员的成绩，他们全部及格了吗？
# 这个问题可以用any和all解决
score = np.random.randint(0, 100, size=20)
score  # array([50, 60, 65, 89, 84, 35, 36, 21, 39, 60,  9, 10, 10, 70, 58, 15, 44, 37, 79, 17])
(score < 60).any()  # 但凡返回True，表示肯定至少有一个人不及格
(score > 60).all()  # 但凡返回True，表示全部都及格了

更多的 ​

python
import numpy as np

np.sin(),np.cos(),np.tan()
python
import numpy as np

# np.around(a, decimals)
"""
a: 数组
decimals: 舍入的小数位数。 默认值为0。 如果为负，整数将四舍五入到小数点左侧的位置
"""
data = np.random.random(size=10)
np.around(data, 3)
"""
array([0.52 , 0.701, 0.972, 0.962, 0.901, 0.573, 0.384, 0.852, 0.38 , 0.887])
"""
python
import numpy as np

a1 = np.random.randint(0, 10, size=3)
a2 = np.random.randint(0, 10, size=3)
display(a1, a2)
"""
array([9, 8, 2])
array([6, 9, 3])
"""
# -------- 加 --------
np.add(a1, a2)  # array([15, 17,  5])

# -------- 减 --------
np.subtract(a1, a2)  # array([ 3, -1, -1])

# -------- 乘 --------
np.multiply(a1, a2)  # array([54, 72,  6])

# -------- 除 --------
np.divide(a1, a2)  # array([1.5       , 0.88888889, 0.66666667])

# -------- 幂运算 --------
np.power(2, 3)  # 8
np.power(a1, 2)  # array([81, 64,  4], dtype=int32)

# -------- 求余运算 --------
np.mode()

# -------- 自然底数的对数 --------
# 自然底数
np.e
np.log()
np.log2()
np.log10()
python
"""
numpy.amin() 和 numpy.amax()，用于计算数组中的元素沿指定轴的最小、最大值。

numpy.ptp():计算数组中元素最大值与最小值的差（最大值 - 最小值）。

numpy.median() 函数用于计算数组 a 中元素的中位数（中值）

标准差std():标准差是一组数据平均值分散程度的一种度量。
	公式：std = sqrt(mean((x - x.mean())**2))
	如果数组是 [1，2，3，4]，则其平均值为 2.5。 因此，
	差的平方是 [2.25,0.25,0.25,2.25]，并且其平均值的平方根除以 4，即 sqrt(5/4) ，结果为 1.1180339887498949。
方差var()：统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数，即 mean((x - x.mean())** 2)。换句话说，标准差是方差的平方根。
"""

矩阵函数 ​

NumPy 中包含了一个矩阵库 numpy.matlib，该模块中的函数返回的是一个矩阵，而不是 ndarray 对象。一个 的矩阵是一个由行（row）列（column）元素排列成的矩形阵列。

  • numpy.matlib.identity() 函数返回给定大小的单位矩阵。单位矩阵是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为 1，除此以外全都为 0。
python
import numpy as np

# eye返回一个标准的单位矩阵
arr = np.eye(6)
arr
"""
array([[1., 0., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0., 0.],
       [0., 0., 1., 0., 0., 0.],
       [0., 0., 0., 1., 0., 0.],
       [0., 0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 0., 1.]])
"""
# 转置矩阵     
arr.T
"""
array([[69, 37, 13,  5, 54],
       [80, 57, 16, 16, 63],
       [ 7, 26, 93, 47, 20],
       [90, 92, 54, 66, 11],
       [31, 91, 87, 51, 94],
       [44, 34, 34, 12, 88]])
"""
# 矩阵相乘，更多参考：https://www.cnblogs.com/alantu2018/p/8528299.html
"""
numpy.dot(a, b, out=None)
a : ndarray 数组
b : ndarray 数组
"""

小练习来了 ​

bash
1. 生成一个Python成绩数组，假设有100人，满分100分，及格60分，如何计算班级的及格率？
2. 随机生成一个一维数组，比较其中是否有至少一个数据大于2倍平均值
3. 如何检查两个形状相同的数组数值是完全一致的？
python
# 1. 生成一个Python成绩数组，假设有100人，满分100分，及格60分，如何计算班级的及格率？
# 生成数组
python = np.random.randint(0, 100, size=100)
python
"""
array([67, 90, 36, 47, 10, 51, 23, 96, 71,  7, 51, 70, 64, 25, 60, 15, 61,
       37, 93, 80, 41, 22, 28, 72,  1, 96, 29, 83, 17, 96, 23, 86, 48, 51,
       93, 34, 85, 23, 94, 30, 52, 54, 18, 84, 70, 29, 56, 59,  7, 47, 13,
       23, 54, 65, 67, 40, 80,  5, 62, 61, 63, 98, 76, 71, 63, 29, 13, 81,
       57, 64, 74, 45, 23, 90, 75, 10, 58, 19, 77, 87, 99, 29, 79, 12, 39,
        4, 49, 14, 93, 73, 92, 10, 43, 26, 96, 21, 19, 94, 17, 63])
"""

# 然后跟60比较，拿到bool类型的数组
python > 60
"""
array([ True,  True, False, False, False, False, False,  True,  True,
       False, False,  True,  True, False, False, False,  True, False,
        True,  True, False, False, False,  True, False,  True, False,
        True, False,  True, False,  True, False, False,  True, False,
        True, False,  True, False, False, False, False,  True,  True,
       False, False, False, False, False, False, False, False,  True,
        True, False,  True, False,  True,  True,  True,  True,  True,
        True,  True, False, False,  True, False,  True,  True, False,
       False,  True,  True, False, False, False,  True,  True,  True,
       False,  True, False, False, False, False, False,  True,  True,
        True, False, False, False,  True, False, False,  True, False,
        True])
"""

# 有了bool类型的数组，对其进行类型转换，最好把bool转为0和1，这样好方便计算
# 怎么转换呢？
# (python > 60).astype(np.int8)  # 方式1
# 方式2，低精度数据跟高精度数据做运算的话，低精度会强制类型转换
# (python > 60) * 1   


# 有了0和1这样的数组，只要求出来，这个数组中1的占比
((python > 60) * 1).mean()  # 0.44
((python > 60) * 1).mean() * 100  # 44.0

# 最终，及格率是44.0%
python
# 2. 随机生成一个一维数组，比较其中是否有至少一个数据大于2倍平均值
data = np.random.randint(0, 50, size=100)
data
"""
array([46, 41, 39,  9, 21, 22, 41, 25, 21, 24, 12,  2,  6, 35, 43, 20, 31,
       33, 32, 46, 26, 48, 36, 38, 37, 45, 20, 30, 18, 14,  3, 40, 41, 44,
       31, 11, 32, 24, 34,  8, 11, 40, 16,  0,  7, 10, 18, 13, 20, 23, 49,
       33, 12,  9, 33, 10,  4, 31,  7, 30, 43, 46,  9,  2, 38, 40, 14, 24,
       16,  0, 10, 13, 36, 25, 20, 32, 49,  5,  7, 40,  2,  5, 22, 19, 45,
       40, 46, 34, 46, 19, 16, 13, 19, 47, 29,  5, 11,  8, 20, 37])
"""

# 求出平均值
data.mean()  # 24.57

# 求出2倍大于平均值的数
data.mean() * 2  # 49.14

# 将整个数组的每个元素都和这个2倍大于平均值的的数进行比较，然后用any计算就行了
data > (data.mean() * 2)
"""
array([False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False])
"""

# any返回True表示数组中包含大于平均值2倍的数
(data > (data.mean() * 2)).any()
python
# 如何检查两个形状相同的数组数值是完全一致的？
a = np.ones(shape=(4,4))
b = np.ones(shape=(4,4))
a, b
"""
(array([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]]),
 array([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]]))
"""

# 两个数组做个比较
a == b
"""
array([[ True,  True,  True,  True],
       [ True,  True,  True,  True],
       [ True,  True,  True,  True],
       [ True,  True,  True,  True]])
"""

# all返回True的话，都表示是完全一致的
(a == b).all()   # True

查找和排序 ​

查找 ​

python
import numpy as np

"""
numpy.argmax() 和 numpy.argmin()
返回指定数组中，匹配到的第一个最大值/最小值元素的索引位置
"""
data = np.random.randint(0, 100, size=10)
data
"""
array([97, 43, 30, 50, 57, 31, 11, 71, 12, 12])
"""
data.argmax(), data.argmin()
"""
(0, 6)
"""
python
import numpy as np

"""
numpy.where() 函数返回输入数组中满足给定条件的元素的索引
"""
data = np.random.randint(0, 100, size=10)
data
"""
array([97, 43, 30, 50, 57, 31, 11, 71, 12, 12])
"""
# 条件表达式
condition = data > 60
"""
array([ True, False, False, False, False, False, False,  True, False, False])
"""
# 根据条件表达式过滤符合条件的结果
np.where(condition)  # (array([0, 7], dtype=int64),)

排序 ​

  • 快速排序，np.sort()与ndarray.sort()都可以，但有区别：

    • np.sort()不改变原始数据，相当于排序结果保存一份新的副本。

    • ndarray.sort()原地处理，不占用空间，但改变原始数据。

  • 索引排序，numpy.argsort() 函数根据数组中每个元素的索引位置大小排序。

  • 部分排序，np.partition(a,k)，有的时候我们不是对全部数据感兴趣，我们可能只对最小或最大的一部分感兴趣。

    • 当k为正时，我们想要得到最小的k个数

    • 当k为负时，我们想要得到最大的k个数

python
import numpy as np

data = np.random.randint(0, 10, size=10)
"""
array([2, 4, 0, 1, 2, 2, 3, 9, 7, 0])
"""
# numpy.sort() 函数返回输入数组的排序副本
new_data = np.sort(data)
display(data, new_data)
"""
array([2, 4, 0, 1, 2, 2, 3, 9, 7, 0])
array([0, 0, 1, 2, 2, 2, 3, 4, 7, 9])
"""

# ndarray.sort()原地处理
display(data)
data.sort()
display(data)
"""
array([2, 4, 0, 1, 2, 2, 3, 9, 7, 0])
array([0, 0, 1, 2, 2, 2, 3, 4, 7, 9])
"""
python
import numpy as np

data = np.random.randint(0, 10, size=5)
"""
array([0, 9, 9, 2, 3])
"""
# numpy.argsort() 函数根据数组中每个元素的索引位置大小排序。
np.argsort(data)
"""
array([0, 3, 4, 1, 2], dtype=int64)
"""
python
import numpy as np

"""
有的时候我们不是对全部数据感兴趣，我们可能只对最小或最大的一部分感兴趣。
	当k为正时，我们想要得到最小的k个数
	当k为负时，我们想要得到最大的k个数
"""
data = np.random.permutation(10)  # 你可以整个比较大的值
"""
array([8, 0, 7, 4, 3, 1, 2, 9, 6, 5])
"""
# 需求是从这个乱序的数组中找到最大的两个数和最小的两个数
# 当k为负时，我们想要得到最大的k个数
np.partition(data, -2)[-2:]  # array([8, 9])
# 当k为正时，我们想要得到最小的k个数
np.partition(data, 2)[:2]  # array([0, 1])